Image Description: The time-independent Schrödinger Equation can be solved to obtain physical values such as the quantized energy of atomic states. The Hamiltonian operator (Ĥ) is particularly important as it represents the total energy of a quantum system. When this operator is applied to a wave function, the energy associated with that state is obtained. The balance between these two terms determines the particle's behavior. In atomic physics, energy is expressed in electronvolts, 1eV=1.602×10−19 Joule.
The Schrödinger Equation, expressed by Erwin Schrödinger (1887-1961) in 1925, plays a central role in understanding atomic structure. It describes the quantum state of electrons in an atom and determines the energy levels associated with each electronic shell and subshell. This approach is based on quantum mechanics, which is fundamentally different from classical descriptions.
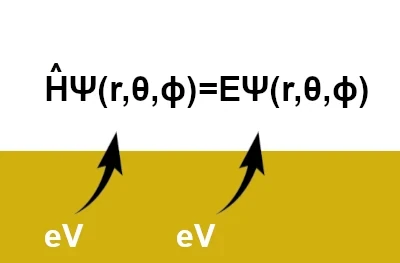
Solving this equation allows us to calculate the discrete energy levels of an atom.
$$\hat{H} \Psi(r, \theta, \phi) = E \Psi(r, \theta, \phi)$$
Note: In quantum mechanics, the atom is often described in spherical coordinates because the electron has a spherical probability distribution around the nucleus, which is very useful for describing the shape and orientation of atomic orbitals.
The electron's energy in hydrogen-like atoms (hydrogen H+, helium He+, lithium Li2+, beryllium Be3+, etc.) is quantized. Energy depends on Z and the principal quantum number n.
$$E_n = -13.6 \, \text{eV} \times \frac{Z^2}{n^2}$$
Single-electron ions are ions with only one electron, all others having been removed. These ions are often used in theoretical models to simplify the study of ionized systems, where the electron may be in different quantized energy levels (possible values of n being 1, 2, 3, etc.).
To ionize a hydrogen atom, that is, to free the electron, an energy of at least 13.6 eV must be supplied to break this bond. To ionize a carbon atom, that is, to free the electron, an energy of at least 489.6 eV is needed to break this bond. Consequently, the closer the electron is to the nucleus, the more negative its energy becomes.
Negative energy in this context reflects the fact that the electron is bound to the atom and cannot escape without an amount of energy being supplied. The potential energy is negative because the electron is attracted to the nucleus. The closer the electron is to the nucleus, the more negative this energy becomes (in other words, the more stable the atom is). The electron's kinetic energy is also negative due to the relationship between the electron's velocity and the force holding it in orbit.
A negative energy indicates that the electron is bound to the nucleus, and positive energy (called ionization energy) must be provided to detach it.
Quantum numbers are parameters used to describe the states of an electron in an atom. There are four main types. These quantum numbers fully characterize an electron's state in an atom and determine its energy levels and spatial configuration.
Shells are sets of orbitals with the same principal quantum number n.
Subshells are subsets of orbitals with the same n and l. Thus, subshells are determined by the secondary quantum number $l$.
The Schrödinger Equation remains one of the essential tools for understanding the properties of atoms and molecules. By defining wave functions, it allows calculation of the discrete energy levels of atoms and ions, providing a clear insight into the structure and properties of matter at the atomic level.
Why is there a limit to cold, but not to heat? 
Galileo's Law of Falling Bodies 
The Ideal Gas Law 
Noether's Theorem: conservation of energy follows from symmetries 
Relationship
between gravitational mass and inertial mass and the equivalence principle 
The Third Essential Equation
in Physics 
The Second Essential Equation
in Physics 
The first essential equation
in physics 
The electromagnetic force or Lorentz force 
The solar energy received depends on
the angle of incidence 
Why is marble colder
than wood? 
Planck's wall theory