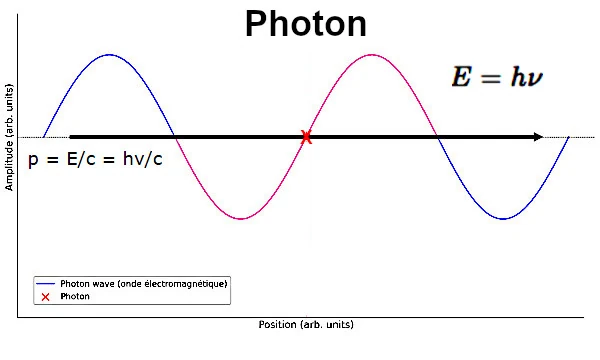
Description of the image: The photon is represented by a sine wave, symbolizing its nature as an electromagnetic wave. The photon's energy is proportional to its frequency (E=hν). The red dot symbolizes the particle aspect of the photon. The photon, on the sine wave, has momentum (p = E/c = hν/c).
The equation E=mc2, proposed by Albert Einstein (1879-1955), establishes a relationship between the mass m and the energy E of an object, with c representing the speed of light in a vacuum.
This equation implies that mass can be converted into energy and vice versa. According to the equation E=mc², it may seem paradoxical that a massless particle (m=0) can have energy (E ≠ 0).
A photon with mass m=0 has energy E≠0 because the equation E=mc2 specifically applies to particles at rest. Indeed, the energy-mass relationship for a particle is given by the complete special relativity equation: E2=(pc)2+(m0c2)2 where p is momentum and m0 is the rest mass.
A photon is a particle without mass and without electric charge. It is the quantum of the electromagnetic field, which means it is an elementary excitation of this field. Its description is governed by Maxwell's equations and, at the quantum level, by the Dirac equation for massless particles.
A photon is therefore defined by its intrinsic nature as a carrier of quantum energy, characterized by its frequency and wavelength. Given that m0=0 for a photon, if it were at rest (v=0), it would imply that its energy E would be zero (since p=0 at v=0). However, the existence of a photon is inseparable from its possession of energy. A photon with zero energy would have no physical meaning and could not exist.
Einstein's theory predicts that there is a universal speed limit, c, which no particle with mass can reach or exceed. This speed corresponds to the speed of light in a vacuum. Thus, for a photon to exist, it must always move at speed c.
Photons are therefore massless particles at rest (m0=0) that always move at the speed of light c. They possess momentum (p) and thus energy.
The relationship between energy and momentum for a photon is given by the equation E=pc.
The energy of a photon is given by Planck's equation E=hν where E is energy, h is Planck's constant (6.626×10^−34J), ν (nu) is the frequency of the photon.
This relationship E=hν shows that the energy of a photon is proportional to its frequency.
By combining the relationship E=pc with Planck's equation, we get p = E/c = hν/c.
In the relativistic context, for moving massive particles, the total energy E is given by the relativistic equation E2=(m0c2)2 + (pc)2.
For photons, the rest mass m is zero, so this equation simplifies to: E=pc.
In summary, although photons have no rest mass, they possess energy and momentum. The energy of a photon is related to its frequency by the equation E=hν, and its momentum is given by p=E/c. The equation E=mc2 applies to particles at rest, but for photons, rest does not exist. The photon is an elementary excitation of the electromagnetic field.
The electromagnetic force or Lorentz force
The solar energy received depends on the angle of incidence
Why is marble colder than wood?
Planck's wall theory