Por que um fóton, que não tem massa, tem energia?

Relação entre Massa e Energia

A equação E=mc², proposta por Albert Einstein (1879-1955), estabelece uma relação entre a massa m e a energia E de um objeto, com c representando a velocidade da luz no vácuo.
Esta equação implica que a massa pode ser convertida em energia e vice-versa. De acordo com a equação E=mc², pode parecer paradoxal que uma partícula sem massa (m=0) possa ter energia (E ≠ 0).
Um fóton com massa m=0 tem energia E≠0 porque a equação E=mc² se aplica especificamente a partículas em repouso. De fato, a relação energia-massa para uma partícula é dada pela equação completa da relatividade especial: E²=(pc)²+(m₀c²)² onde p é o momento e m₀ é a massa em repouso.

Impossibilidade de Repouso para um Fóton

O fóton é uma partícula sem massa e sem carga elétrica. É o quantum do campo eletromagnético, o que significa que é uma excitação elementar desse campo. Sua descrição é governada pelas equações de Maxwell e, no nível quântico, pela equação de Dirac para partículas sem massa.
Um fóton é, portanto, definido por sua natureza intrínseca como portador de energia quântica, caracterizada por sua frequência e comprimento de onda. Dado que m₀=0 para um fóton, se ele estivesse em repouso (v=0), isso implicaria que sua energia E seria nula (já que p=0 em v=0). No entanto, a existência de um fóton é inseparável da sua posse de energia. Um fóton com energia nula não teria sentido físico e não poderia existir.
A teoria de Einstein prevê que existe um limite de velocidade universal, c, que nenhuma partícula com massa pode alcançar ou superar. Essa velocidade corresponde à velocidade da luz no vácuo. Assim, para que um fóton exista, ele deve sempre se mover à velocidade c.

Energia e Fótons

Os fótons são, portanto, partículas de luz sem massa em repouso (m₀=0) que sempre se movem à velocidade da luz c. Eles possuem quantidade de movimento (p) e, portanto, energia.
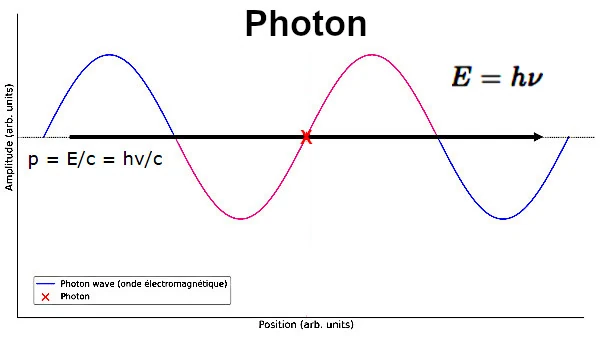
A relação entre a energia e a quantidade de movimento para um fóton é dada pela equação E=pc.
A energia de um fóton é dada pela equação de Planck E=hν onde E é a energia, h é a constante de Planck (6.626×10^−34J), ν (nu) é a frequência do fóton.
Essa relação E=hν mostra que a energia de um fóton é proporcional à sua frequência.

Combinando a relação E=pc com a equação de Planck, obtemos p = E/c = hν/c.

No contexto relativístico, para partículas massivas em movimento, a energia total E é dada pela equação relativística E²=(m₀c²)² + (pc)².
Para os fótons, a massa em repouso m é nula, então essa equação se simplifica para: E=pc.

Conclusão

Em resumo, embora os fótons não tenham massa em repouso, possuem energia e quantidade de movimento. A energia de um fóton está relacionada à sua frequência pela equação E=hν, e sua quantidade de movimento é dada por p=E/c. A equação E=mc² aplica-se a partículas em repouso, mas para os fótons o repouso não existe. O fóton é uma excitação elementar do campo eletromagnético.