A que distância fica o horizonte?

Compreender a distância aparente do horizonte

O horizonte é o limite aparente entre a Terra e o céu. Sua distância depende da curvatura terrestre, da altura do observador e da refração atmosférica. Esta distância pode ser calculada por meio de uma fórmula geométrica simples sem considerar a refração atmosférica.

Distância geométrica simples ao horizonte

A distância ao horizonte, em uma Terra ideal perfeitamente esférica e sem atmosfera, é calculada por \(\,d = \sqrt{2Rh + h^2}\,\) onde \(R\) é o raio terrestre (\(\approx 6371\) km) e \(h\) a altura do observador. Por exemplo, a 2 m de altura, o horizonte geométrico fica a cerca de 5 km.

Cálculo detalhado da distância ao horizonte

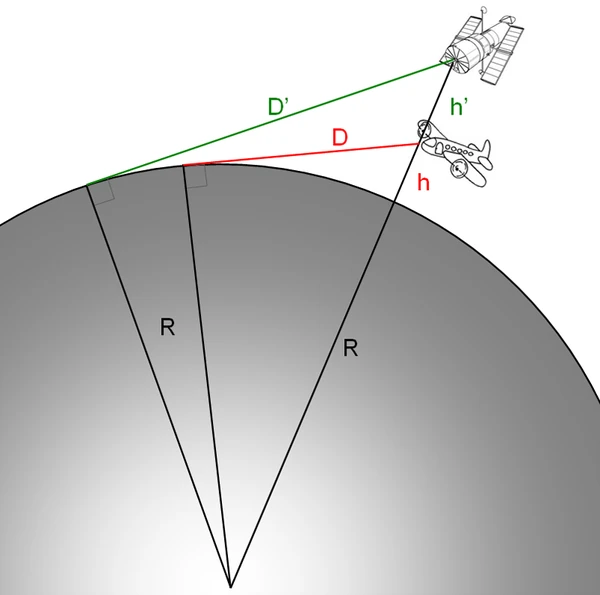
Consideremos um observador situado a uma altura \(h\) acima da superfície terrestre. Seja \(R\) o raio médio da Terra (\(R \approx 6371\) km). A reta que liga o olho do observador ao ponto de tangência na superfície é perpendicular ao raio terrestre nesse ponto. O triângulo formado pelo centro da Terra, o ponto de tangência e o observador é retângulo. Aplicando o teorema de Pitágoras: \( (R + h)^2 = R^2 + d^2 \) onde \(d\) é a distância em linha reta entre o observador e o horizonte. A distância no solo, seguindo a curvatura, é: \( s = R \cdot \theta \) com \(\theta = \arccos\left( \frac{R}{R+h} \right)\). Combinando: \( s = R \cdot \arccos\left( \frac{R}{R+h} \right) \) e para \(h \ll R\), obtemos a aproximação: \( s \approx \sqrt{2Rh + h^2} \)

Cálculo da distância ao horizonte com correção atmosférica

Na realidade, a refração atmosférica aumenta ligeiramente essa distância, pois os raios de luz são curvados em direção ao solo. Em condições padrão, modela-se esse efeito substituindo \(R\) por \(R / (1 - k)\) com \(k \approx 0{,}13\).

Tabela comparativa das distâncias ao horizonte conforme a altitude

N.B.:
O horizonte terrestre nunca existe completamente a partir do momento em que se deixa a superfície: quanto mais se sobe, maior a porção visível da Terra. Da ISS (408 km), avista-se cerca de 3,2% da superfície total (≈9 milhões de km²). Em órbita geoestacionária (36.000 km), vê-se exatamente metade do planeta. Para observar 99% da superfície de uma só vez, seria necessário atingir cerca de 21.700 km de altitude. Além disso, o horizonte recua praticamente até a borda oposta da Terra, mas só desaparece totalmente a uma distância infinita.