最終更新日: 2025 年 8 月 14 日

地平線はどれくらい遠いですか？

地平線までの距離を計算するスキーム — *大気のない理想的な完全な球形の地球上の、観測者と地平線の間の幾何学形状を示す図。画像出典:astronoo.com*

地平線からの見かけの距離を理解する

地平線は地球と空の間の明らかな境界です。その距離は地球の曲率、観測者の高さ、大気の屈折によって決まります。この距離は、大気の屈折を考慮せずに、単純な幾何学的公式を使用して計算できます。

地平線からの単純な幾何学的距離

大気のない理想的な完全な球形の地球上での地平線までの距離は、\(\,d = \sqrt{2Rh + h^2}\,\) によって計算されます。ここで、\(R\) は地球の半径 (\(\約 6371\) km)、\(h\) は観測者の高さです。たとえば、高さ 2 m では、幾何学的な地平線は次のようになります。約5km。

地平線からの距離の詳細な計算

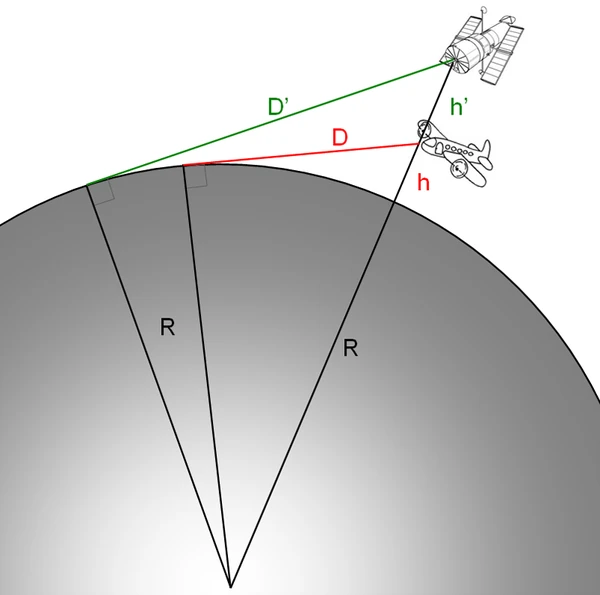
地球の表面から \(h\) の高さに観測者がいるとします。 \(R\) を地球の平均半径 (\(R \約 6371\) km) とします。観察者の目と表面上の接点を結ぶ線は、その点での地球の半径に対して垂直です。地球の中心、接点、観測者によって形成される三角形は直角です。ピタゴラスの定理を適用すると、次のようになります。 \( (R + h)^2 = R^2 + d^2 \) ここで \(d\) は観測者と地平線の間の直線距離です。曲率に従った地面までの距離は次のとおりです。 \( s = R \cdot \θ \) \(\theta = \arccos\left( \frac{R}{R+h} \right)\) となります。以下を組み合わせることで、 \( s = R \cdot \arccos\left( \frac{R}{R+h} \right) \) \(h \ll R\) については、次の近似値が得られます。 \( s \およそ \sqrt{2Rh + h^2} \)

大気補正による地平線距離の計算

実際には、光線が地面に向かって曲がるため、大気の屈折によってこの距離はわずかに増加します。標準条件では、\(R\) を \(R / (1 - k)\) を \(k \ほぼ 0{,}13\) に置き換えることによってこの効果をモデル化します。

高度別地平線からの距離の比較表

観測者の位置に応じた地平線までの距離
状況	目の高さ (m)	幾何学的距離 (km)	屈折距離(km)	仮説
立っている人	2	5.06	5.24	標準大気、\(k=0{,}13\)
ビルの3階にいる人	10	11.28	11.68	3階建ての高さの目安（3.3m/階）
100メートルの崖	100	35.68	36.90	穏やかな海、最高の透明度
1000メートルの山	1000	112.88	116.55	晴れた頂上
高度10,000メートルの飛行機	10000	357.10	368.26	標準大気圏での飛行
ISS 宇宙ステーション (~408 km)	408000	2270.00	2336.00	対流圏の上の眺め
静止軌道 (~36,000 km)	36000000	19040.00	19300.00	静止軌道からの眺め、地球の半分が見える

注： :
私たちが地表を出た瞬間から、地球の地平線が完全に存在することはありません。高度に行けば行くほど、地球の目に見える部分は大きくなります。 ISS (408 km) からは、総表面 (約 900 万 km2) の約 3.2% が見えます。静止軌道 (36,000 km) では、地球のちょうど半分が見えます。地表の 99% を一目で観察するには、高度約 21,700 km に到達する必要があります。それを超えると、地平線はほぼ地球の反対側の端まで後退しますが、完全に消えるのは無限の距離だけです。