物理学の第一方程式：力を数学的に表現する方法

力学の基本原理

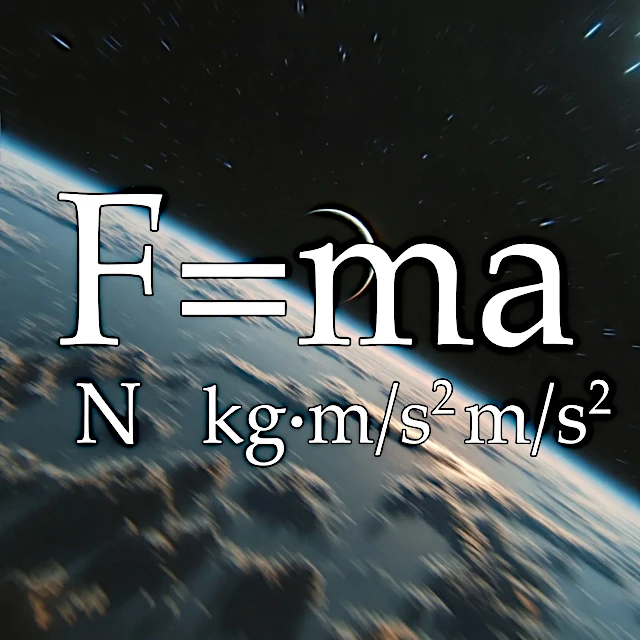
最も基本的で普遍的に認知されている方程式は、ニュートンの第二法則（1643-1727）です。

F=maは、物理学、特に古典力学における基本的な方程式です。これは、3つの本質的な物理量の間の関係を表しています：
• $ \vec{F} $ は物体に加えられる力で、単位はニュートン（N）です、
• m は物体の質量で、単位はキログラム（kg）です、
• a は物体の加速度で、単位はメートル毎秒毎秒（m/s²）です。

この方程式は、物体に加えられる力、その物体の質量、そしてその結果生じる加速度の関係を説明しています。古典力学と物体の運動をつなぐ重要な方程式であり、物理学の多くの他の方程式や概念の基礎となっています。

注： ニュートンの第一法則（慣性の法則）は、物体に正味の力が働かないときの物体の振る舞いを説明する物理学の基本概念です。 ニュートンの第一法則には単一の方程式は存在しません。

力とは何ですか?

力の概念は、古典物理学、特にニュートン力学の文脈における基本概念の 1 つです。これは、オブジェクトに作用したときに、このオブジェクトの動きの状態を変更する相互作用として定義されます。この力により、対象の物体が加速したり、方向を変えたり、変形したりする可能性があります。
古典力学の形式主義では、力 $ \vec{F} $ はベクトル量、つまり方向、意味、強度を持つ量です。

F=ma は私たちに何を伝えますか?

力は加速度に比例します。適用される力が大きくなるほど、物体の加速度も大きくなります。
質量は加速に抵抗します。物体の質量が大きいほど、物体を動かしたり、速度を変更したりする（つまり、加速させる）ことが難しくなります。

言い換えれば、F=ma は、物体の動きを変える (動きを開始する、停止する、方向や速度を変える) には、物体に力を加えなければならないことを示しています。

F=ma の極限

F=ma は単純化したものであることに注意することが重要です。これは古典力学の枠組み内で、光速をはるかに下回る速度に対して有効です。非常に高速にするには、アインシュタインの特殊相対性理論を使用する必要があります。さらに、この方程式は摩擦力などの特定の力を考慮していません。