量子不確実性: ハイゼンベルク原理の重要な役割

画像の説明: ハイゼンベルクの不確定性原理は、量子力学の基礎です。それは、粒子の位置と運動量あるいは運動量（\(\vec{p} = m \cdot \vec{v}\)）を同時に正確に知ることは不可能であるということです。 画像出典:astronoo.com

アインセンベルグの公式

の式ヴェルナー・アインセンベルク(1901-1976) は、以下の根本的な発見です。量子力学。 1927 年に策定されたこの規則は、位置 (x) と運動量 (p) などの物理的特性の特定のペアを同時に知ることができる精度に対する基本的な制限を表します。

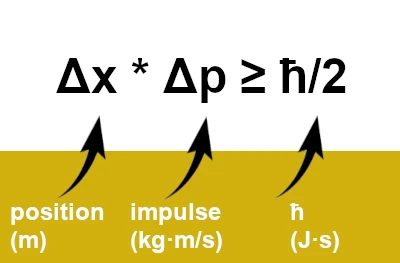
ハイゼンベルクは、粒子の位置をより正確に測定すればするほど、粒子の運動量を正確に知ることができなくなり、その逆も同様であることを示しました。この関係は数学的に次の不等式で表されます: Δx * Δp ≥ ħ/2、ここで \(\hbar = \frac{h}{2\pi}\) (h = プランク定数、ħ = 換算プランク定数)。

用語の解釈

\(\Delta x\): 粒子の位置の不確実性。

\(\Delta p\): 運動量 \(p = m v\) の不確実性。\(m\) は質量、\(v\) は速度です。

\(\hbar \about 1.054 \times 10^{-34}\, \text{J.s}\) は換算されたプランク定数です。

この不等式は、これら 2 つの不確実性の積が \(\frac{\hbar}{2}\) で与えられる制限を下回らないことを意味します。

つまり、粒子の位置 \(\Delta x\) の不確実性を小さくすると、粒子の運動量 \(\Delta p\) の不確かさが増加し、その逆も同様です。

注： :
量子粒子のメートル単位の位置は、空間の特定の領域に位置する粒子の特定の座標が存在しないことで説明されますが、ハイゼンベルクの不確定性原理により、特定の時間における粒子の正確な位置は確率的に記述されます。

ハイゼンベルクの不確定性原理の考え方を視覚化する例

高速で走行する車の鮮明な写真を撮ろうとしているところを想像してみてください。鮮明な画像を取得するには、非常に短い露光時間を使用する必要があります。ただし、露光時間が短いと取り込む光が少なくなり、光が不十分な場合には画像が暗くなったり、ぼやけたりする可能性があります。

• 正確な位置（鮮明な写真）: 車の非常に鮮明な写真を撮ることができれば、正確な瞬間にその位置を捉えたことになります。ただし、露出時間が短いため、動きのコンテキストのないスナップショットのみが表示されるため、動き (速度) に関する情報が少なくなります。
• 正確な動き（ぼやけた写真）: より多くの光を取り込み、より明るい画像を取得するために露光時間を長くすると、露光中に車が動くため、車がぼやけて見えます。そうすれば、動きに関するより多くの情報が得られます (方向と速度を示すブレが表示されます) が、特定の瞬間における車の正確な位置の精度は失われます。

現代物理学への影響

• 量子スケールの現実：不確定性原理により、システムの進化を正確に予測することが可能になりました。この原理は、量子スケールの現実は本質的に確率的であることを示しています。彼は古典物理学の決定論的な見方を確率論的な枠組みに置き換えました。
• 波動関数の減少: 不確実性は、量を測定するとシステムが混乱する可能性があることを意味し、「客観的な観察者」という概念が問題になります。 「波動関数の低減」という概念は、測定によってシステムの波動関数が規定の状態に「崩壊」するという仮定を置き、部分的には不確定性原理の結果として登場しました。
• エネルギーの定量化: 不確定性原理は、原子 (ボーアモデル) や分子などの系におけるエネルギーの定量化などの現象を説明するために重要です。量子効果は、超伝導や超流動などの巨視的な現象に影響を与えます。
• トンネル効果: 不確実性原理は、トンネル効果を説明するための基礎でもあります。トンネル効果とは、古典物理法則に従って粒子がエネルギー障壁を通過するのに十分なエネルギーを持たない場合でも、エネルギー障壁を通過する確率がゼロではないという量子現象です。この現象は、トンネル トランジスタや走査トンネル顕微鏡などのデバイスで使用されます。
• 量子真空: 不確実性のため、量子真空 (系の基底状態) であっても完全に「空」ではなく、量子ゆらぎの影響を受けます。
• 波動粒子の二重性: 不確実性は、量子物体 (電子や光子など) が波と粒子として同時にどのように振る舞えるかを説明する波動粒子双対性と密接に関係しています。位置と勢いに関する不確実性は、この二重性の直接的な現れです。