最終更新日: 2023 年 4 月 7 日

マクスウェル方程式

マクスウェルの 4 方程式

マクスウェルは 1865 年に初めて、20 個の未知数を含む 20 個の方程式の形で理論を発表し、その後 1873 年に 8 個の方程式の形で理論を書き直しました。 Oliver Heaviside (1850-1925) がこれらの方程式を 4 つのベクトルおよびスカラー方程式の形で再定式化したのは 1884 年になってからでした。

したがって、マクスウェル方程式は、電気と磁気を理解する上で不可欠な電磁場の基本特性を記述する 4 つの数学方程式のセットです。
電界E⃗ρ で示される粒子によって作成されます。
磁場B⃗は電流、つまり J で示される電荷の移動によって生成されます。銅線に電流が流れると磁場が発生します（この電流により近くにあるコンパスの針がずれます）。
多くの現象は電気的かつ磁気的です（光、静電気、電池、電磁誘導、電磁石などを含む波動）。

マクスウェル方程式は、電磁場を表すためにベクトル表記で書かれることがよくあります (E⃗そしてB⃗）。

• マクスウェルの最初の方程式は、ガウスの法則とも呼ばれ、電気の流れが閉じた表面をどのように通過するかを説明します。
∇.E = ρ/ε0
∇.E は電界発散であり、特定の表面から出る電束の量を測定します。
ρ は考慮した領域の電荷密度、ε0 は物理定数である真空の誘電率です。

• マクスウェルの 2 番目の方程式は、磁気に関するガウスの法則とも呼ばれ、閉じたガウス面を通る全磁束が常に 0 であると述べています。
∇.B = 0
∇.B は磁場の発散で、特定の表面から出る磁束の量を測定します。

• マクスウェルの 3 番目の方程式は、ファラデーの法則とも呼ばれ、移動する磁場がどのように電場を生成するかを説明します。
∇ × E = -dB/dt
∇ x E は電場の回転であり、特定のループの周りの電場の循環を測定します。
dB/dt は磁場の時間的変化です。

• マクスウェルの 4 番目の方程式は、アンペール・マクスウェルの法則とも呼ばれ、移動する電場が磁場をどのように生成するかを説明します。
∇ x B = μ0(J + ε0*dE/dt)
∇ x B は回転磁場であり、特定のループの周りの磁場の循環を測定します。
μ0 は真空透過率であり、これも物理定数です。
J は考慮した領域の電流密度、dE/dt は電場の時間的変化です。

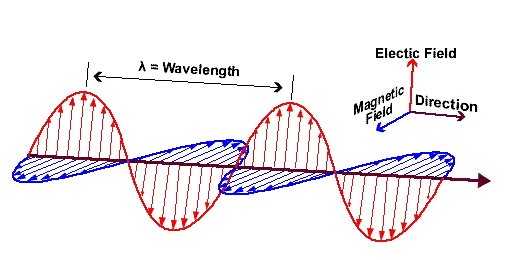
マクスウェルの法則は、電界と磁界の挙動とその 2 つの関係を説明します。したがって、マクスウェルの方程式は、運動中に電場と磁場がどのように相互に生成されるかを説明します。