Equações de Maxwell

4 equações de Maxwell

Maxwell publicou pela primeira vez em 1865 sua teoria na forma de vinte equações com vinte incógnitas, então em 1873 ele reescreveu sua teoria na forma de oito equações. Não foi até 1884 que Oliver Heaviside (1850-1925) reformulou essas equações na forma das quatro equações vetoriais e escalares.

As equações de Maxwell são, portanto, um conjunto de quatro equações matemáticas que descrevem as propriedades fundamentais dos campos eletromagnéticos, essenciais para entender a eletricidade e o magnetismo.
O campo elétrico E⃗ é criado por partículas denotadas por ρ.
O campo magnético B⃗ é criado por correntes, ou seja, cargas em movimento, denotadas por J. Quando uma corrente passa por um fio de cobre, um campo magnético é criado (essa corrente desvia a agulha de uma bússola colocada nas proximidades).
Muitos fenômenos são elétricos e magnéticos (ondas incluindo luz, eletrostática, baterias, indução eletromagnética, eletroímãs, etc.)

As equações de Maxwell são frequentemente escritas em notação vetorial para representar campos eletromagnéticos (E⃗ e B⃗).

• A primeira equação de Maxwell, também chamada de lei de Gauss, descreve como o fluxo elétrico passa por uma superfície fechada.
∇.E = ρ/ε0
∇.E é a divergência do campo elétrico, que mede a quantidade de fluxo elétrico que sai de uma determinada superfície.
ρ é a densidade de carga elétrica na região considerada, e ε0 é a permissividade do vácuo, que é uma constante física.

• A segunda equação de Maxwell, também chamada de lei de Gauss para o magnetismo, afirma que o fluxo magnético total que passa por uma superfície gaussiana fechada é sempre zero.
∇.B=0
∇.B é a divergência do campo magnético, que mede a quantidade de fluxo magnético que sai de uma determinada superfície.

• A terceira equação de Maxwell, também chamada de lei de Faraday, descreve como um campo magnético em movimento pode criar um campo elétrico.
∇ x E = -dB/dt
∇ x E é o rotacional do campo elétrico, que mede a circulação do campo elétrico em torno de um determinado loop.
dB/dt é a variação temporal do campo magnético.

• A quarta equação de Maxwell, também chamada de lei de Ampere-Maxwell, descreve como um campo elétrico em movimento pode criar um campo magnético.
∇ x B = μ0(J + ε0*dE/dt)
∇ x B é o rotacional do campo magnético, que mede a circulação do campo magnético em torno de um determinado loop.
μ0 é a permeabilidade ao vácuo, que é outra constante física.
J é a densidade de corrente elétrica na região considerada, e dE/dt é a variação temporal do campo elétrico.

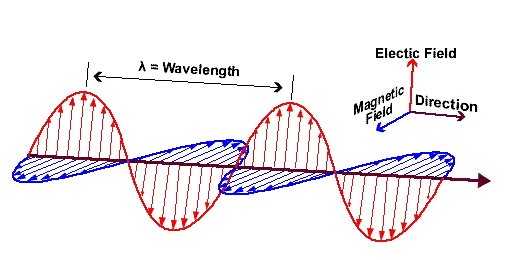
As leis de Maxwell descrevem o comportamento dos campos elétrico e magnético e a relação entre os dois. Assim, as equações de Maxwell descrevem como os campos elétricos e magnéticos podem criar um ao outro em movimento.