Descrição da imagem: O túmulo de Ludwig Eduard Boltzmann (1844-1906) no Zentralfriedhof, Viena, com seu busto e sua fórmula da entropia.
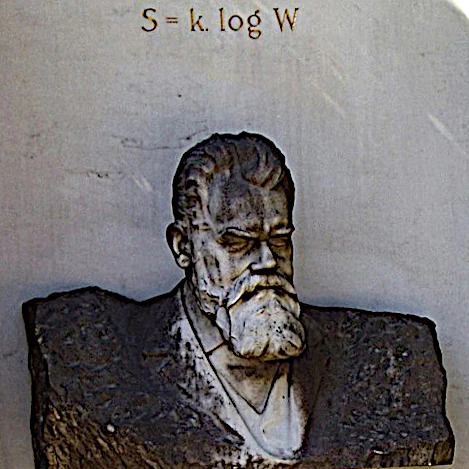
A Equação da Entropia foi desenvolvida pelo físico austríaco Ludwig Boltzmann. A entropia (S) é um conceito poderoso que mede a desordem ou a incerteza de um sistema físico.
A equação da entropia de Boltzmann é essencial para entender a relação entre a entropia e as propriedades termodinâmicas de um sistema, como temperatura, pressão e energia. Ela desempenha um papel crucial no estudo dos processos de equilíbrio termodinâmico, na evolução dos sistemas físicos e na interpretação estatística das leis da termodinâmica.
A equação da entropia de Boltzmann geralmente é expressa da seguinte forma: S = k log(W)
Essa equação mostra que a entropia é proporcional ao logaritmo do número de microestados possíveis do sistema.
Um sistema é considerado de alta entropia se puder existir em um grande número de microestados desordenados (mais desordem), enquanto um sistema com poucos microestados acessíveis terá uma entropia menor (mais ordem).
O logaritmo transforma grandes valores em valores menores, facilitando certos cálculos em física e matemática. Se usássemos ���� diretamente na equação de Boltzmann, obteríamos valores de entropia enormes e difíceis de interpretar. O logaritmo serve para tornar esses valores mais manejáveis e respeitar propriedades matemáticas essenciais, como a aditividade da entropia. Em resumo, mesmo que um logaritmo seja "muito menor," ele nos dá uma escala mais prática para raciocinar sobre sistemas onde o número de microestados é gigantesco. É um pouco como medir distâncias astronômicas em anos-luz em vez de quilômetros!
A equação de Boltzmann não levou diretamente à descoberta do átomo, mas desempenhou um papel crucial na compreensão teórica da natureza atômica da matéria e no desenvolvimento da física estatística, que confirmou a existência dos átomos.
S = klog(W) relaciona o comportamento microscópico (movimento dos átomos) com as propriedades macroscópicas (pressão, temperatura, entropia).
A entropia é um conceito fundamental utilizado em diversas áreas da ciência, incluindo termodinâmica, mecânica estatística, teoria da informação, ciência da computação, ciência da complexidade e outros campos.
A definição de entropia pode variar ligeiramente dependendo do contexto, mas compartilha ideias comuns nesses campos.
Em todos os casos, a entropia é uma medida da quantidade de informação, desordem, diversidade ou incerteza em um sistema.
No entanto, no universo, observamos estruturas cada vez mais ordenadas que se formam a partir de processos inicialmente menos organizados. Isso parece contradizer a ideia intuitiva de que a entropia, como medida da desordem, deve sempre aumentar, conforme sugerido pelo segundo princípio da termodinâmica.
O aumento da ordem local (como a formação de galáxias e estrelas) não implica uma violação do segundo princípio da termodinâmica. Esse princípio se aplica a todo o sistema e estabelece que a entropia total de um sistema isolado, o Universo, não pode diminuir ao longo do tempo.
Quando observamos a formação de galáxias e estrelas, devemos considerar todo o sistema, incluindo a energia e os processos envolvidos em grande escala. Assim, o que pode parecer uma diminuição da desordem em pequena escala é, na verdade, uma simples redistribuição de energia e entropia em uma escala maior.
As estruturas que emergem no Universo não são anomalias, mas manifestações de processos físicos fundamentais, onde a organização local sempre é acompanhada pela dissipação de energia em outro lugar.
A dissipação de energia ocorre principalmente na forma de radiação térmica. Quando uma estrutura ordenada se forma localmente, como uma estrela ou galáxia, o sistema global aumenta sua entropia, por exemplo:
Em resumo, o Universo equilibra a criação de estruturas ordenadas redistribuindo energia na forma de radiação e outros processos dissipativos, garantindo que o segundo princípio da termodinâmica seja sempre respeitado. Longe de ser uma ilusão, essa ordem aparente é uma faceta natural do caos cósmico.
Como os Painéis Solares Injetam Eletricidade na Rede? 
Dinâmica do Momentum para explicar a propulsão de foguetões ou medusas 
Distribuição Energética dos Elétrons em Átomos 
Princípio da Incerteza de Heisenberg: Compreendendo a Incerteza Quântica 
Relação entre Energia, Potência e Tempo 
Por que existe um limite para o frio, mas não para o calor? 
A Lei da Queda dos Corpos de Galileu 
A Lei dos Gases Ideais 
Equação de Schrödinger e Estrutura dos Átomos 
Teorema de Noether: a conservação da energia surge de simetrias 
Relação entre massa gravitacional e massa inercial e o princípio da equivalência 
A Terceira Equação Essencial em Física 
A Segunda Equação Essencial em Física 
A primeira equação essencial em física 
A força eletromagnética ou força de Lorentz 
A energia solar recebida varia dependendo da inclinação 
Por que o mármore é mais frio que a madeira? 
Teoria do muro de Planck