Imagem: O físico teórico britânico Paul Dirac (1902-1984) em 1928 formulou esta equação sobre o comportamento de partículas de alta energia.
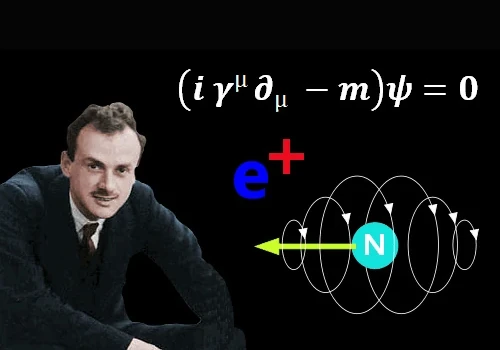
A equação de Dirac foi formulada pelo físico teórico britânico Paul Dirac (1902-1984) em 1928.
A equação de Dirac é importante na física quântica porque é capaz de descrever o comportamento de partículas de alta energia que se movem a velocidades próximas à da luz, como os elétrons, que não podem ser descritos com precisão pelas equações da física clássica. Nesta equação, Dirac combina a mecânica quântica e a teoria especial da relatividade de Albert Einstein.
A equação de Dirac teve um impacto significativo na física quântica e levou a muitas descobertas importantes, como a previsão da existência de antimatéria.
É mais geral do que a equação de Schrödinger, que só se aplica a partículas não relativísticas.
Ela também introduziu a noção de spin (momento angular intrínseco) das partículas, que é uma propriedade fundamental das partículas subatômicas.
Também possibilitou a compreensão de fenômenos como a polarização do vácuo, que é a criação espontânea de pares partícula-antipartícula a partir do vácuo quântico.
A equação de Dirac é escrita: (iγ^μ∂_μ-mc)ψ=0
• I é o
• γ^μ representa uma matriz gama que depende de um índice μ. As matrizes gama são matrizes de dimensão 4x4 (quatro dimensões do espaço-tempo) usadas para representar as propriedades de
• ∂_μ é o operador de derivada parcial em relação à coordenada espaço-tempo μ (∂/∂xμ) = (∂/∂t, ∂/∂x, ∂/∂y, ∂/∂z). Este operador de derivada parcial é usado para descrever como um campo físico, como o campo eletromagnético ou o campo gravitacional, varia no espaço-tempo levando em consideração os efeitos relativísticos.
• m é a massa da partícula.
• é a velocidade da luz no vácuo.
• ψ é a função de onda que descreve o estado quântico da partícula.
Para que serve a equação de Dirac?
• A equação de Dirac é usada na teoria quântica de campos para descrever as interações entre partículas elementares, tornando-a uma ferramenta matemática essencial para a física de partículas.
• A descoberta da existência de antipartículas, em particular a do positrão (antipartícula do eletrão) permite a sua utilização em imagiologia médica.
De fato, a tomografia por emissão de pósitrons consiste em injetar no paciente um fármaco radiofármaco cujo isótopo radioativo é um emissor de radiação β+, ou seja, um emissor de pósitrons. Esses pósitrons são imediatamente aniquilados ao entrar em contato com os elétrons dos tecidos circundantes, gerando dois fótons gama. A detecção desses fótons permite localizar o local de sua emissão e a concentração do traçador em cada ponto dos órgãos.
• Permite explicar a estrutura fina das linhas espectrais do hidrogênio. Essas linhas brilhantes que aparecem no espectro de emissão ou absorção de um elemento químico são causadas pela transição de elétrons entre diferentes níveis de energia nos átomos.
• É útil em colisores elétron-pósitron que aceleram simultaneamente dois feixes de partículas em direções opostas, um de elétrons e outro de pósitrons. Durante essas colisões frontais de alta energia, os elétrons e pósitrons se aniquilam, liberando uma energia considerável capaz de criar novas partículas.
A equação de Dirac inspirou outras equações, como a de Klein-Gordon, que descreve partículas sem spin (bósons), como os fótons. Em conclusão, foi um dos maiores desenvolvimentos na física teórica do século 20 e expandiu nossa compreensão do universo. é possível que os primeiros humanos a chegarem a Marte o façam a bordo de uma espaçonave de pósitrons.
Por que existe um limite para o frio, mas não para o calor? 
A Lei da Queda dos Corpos de Galileu 
A Lei dos Gases Ideais 
Equação de Schrödinger e Estrutura dos Átomos 
Teorema de Noether: a conservação da energia surge de simetrias 
Relação entre massa gravitacional e massa inercial e o princípio da equivalência 
A Terceira Equação Essencial em Física 
A Segunda Equação Essencial em Física 
A primeira equação essencial em física 
A força eletromagnética ou força de Lorentz 
A energia solar recebida varia dependendo da inclinação 
Por que o mármore é mais frio que a madeira? 
Teoria do muro de Planck