A equação de Schrödinger revolucionou nossa visão da matéria

Da certeza à probabilidade: o átomo segundo Schrödinger

Imagine por um momento que, no átomo, o elétron não é mais um pequeno planeta girando ordenadamente em torno de um núcleo-sol, mas uma nota musical, uma vibração, uma onda. Esta é a revolução conceitual desencadeada por Erwin Schrödinger (1887-1961) em 1926.

A equação de Schrödinger (equação fundamental da mecânica quântica que descreve a evolução de uma partícula por uma função de onda.) não nos diz onde o elétron está com certeza, mas onde é provável que ele esteja. Ela transforma o espaço atômico possível em uma pista de dança onde as figuras do dançarino desenham os orbitais prováveis.

Entendendo a equação de Schrödinger sem complicações

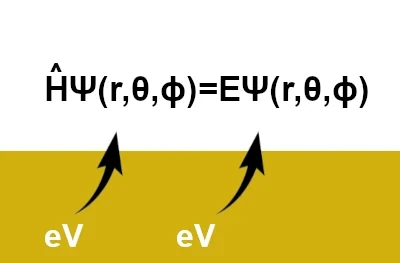
A equação de Schrödinger é escrita como: \(\hat{H}\,\Psi(r,\theta,\phi)=E\,\Psi(r,\theta,\phi)\) onde \((r, \theta, \phi)\) são coordenadas esféricas (r: coordenada radial, θ: coordenada polar, ϕ: coordenada azimutal). No entanto, em sua forma mais simples, ela é escrita como: \( \hat{H} \Psi = E \Psi \)

Para desvendar os mistérios do átomo, é necessária uma chave especial. Esta chave é o que os físicos chamam de "função de onda". Ela tem um nome elegante: Ψ (pronuncia-se "Psi", como o início de "psique" ou o tridente de Netuno).

Como ler simplesmente \( \hat{H} \Psi = E \Psi \)?

Imagine que Ψ é uma espécie de "mapa de navegação" para o elétron. Este mapa não diz para onde o elétron irá, mas onde ele pode ir. Mais precisamente, ele descreve os lugares onde você tem chances de encontrá-lo e os lugares onde não o encontrará.

À esquerda, \(\hat{H}\) representa "tudo o que acontece no átomo" (a atração do núcleo, a energia, as restrições). À direita, \(E\) é o resultado: a energia que o elétron deve ter para ser estável nesta configuração.

Resolver esta equação é como procurar a nota certa em um piano para que ela ressoe perfeitamente em um cômodo. Não se pode tocar qualquer coisa: apenas certas notas (energias \(E\)) e certas maneiras de vibrar (funções Ψ) funcionam harmonicamente.

Mas como é Ψ?

Este foi o grande dilema dos físicos até que Max Born (1882-1970) teve uma intuição brilhante. Ele disse: "Não olhem para Ψ em si, olhem para seu reflexo, seu quadrado, \(|\Psi|^2\)". É como a fumaça que revela uma nuvem de probabilidade onde o objeto estava antes do mágico fazê-lo desaparecer. Assim, \(|\Psi|^2\) nos indica, ponto a ponto no espaço ao redor do núcleo, a probabilidade de presença do elétron.

Em resumo, onde \(|\Psi|^2\) é grande é o "jardim" do átomo, onde o elétron passa seu tempo. Onde \(|\Psi|^2\) é zero, é um "deserto", o elétron nunca vem. O elétron se torna então menos uma bolinha e mais uma nuvem, um rastro de luz, uma dança difusa e elegante ao redor do núcleo chamada "orbital".

Os padrões da dança eletrônica: os orbitais atômicos

Aplicada ao átomo de hidrogênio (um próton e um elétron), a equação de Schrödinger revela uma série de soluções, estados quânticos, cada um caracterizado por três números, frequentemente chamados de números quânticos. Cada solução corresponde a um orbital atômico, uma forma geométrica tridimensional específica que é a "zona de dança" privilegiada do elétron.

Onde Niels Bohr (1885-1962) via elétrons girando em órbitas circulares bem arrumadas, como planetas ao redor do Sol, a equação de Schrödinger revela um universo muito mais rico e poético. As soluções desenham no espaço formas geométricas de elegante complexidade.

• A esfera perfeita (orbital s): A mais simples delas, chamada 1s, é uma esfera. O elétron não tem direção preferida; ele está presente de maneira homogênea ao redor do núcleo, como uma névoa perfeitamente simétrica.
• Os halteres (orbitais p): Assim que nos afastamos um pouco do núcleo (segundo nível de energia), o espaço se estrutura. Aparecem então três formas idênticas em "haltere", cada uma apontando em uma direção do espaço (ao longo dos eixos x, y e z). O elétron se concentra então em dois lóbulos opostos, de cada lado de uma zona de silêncio (o plano nodal).
• As flores da matéria (orbitais d e f): Em distâncias ainda maiores, a coreografia se enriquece. Os orbitais d adotam geometrias que evocam trevos de quatro folhas. Os orbitais f, por sua vez, desdobram pétalas múltiplas em arranjos ainda mais sofisticados. Verdadeiras assinaturas matemáticas do espaço, eles são para a química o que as escalas são para a música: a estrutura fundamental que permite todas as combinações, todas as moléculas, toda a matéria que nos cerca.

Essas formas não são meras fantasias matemáticas. Elas são a pedra angular da química. A geometria dos orbitais determina como os átomos podem se ligar entre si para formar moléculas. A direção dos orbitais p, por exemplo, explica a forma angular da molécula de água (H₂O). A riqueza dos orbitais d é responsável pelas cores brilhantes dos íons dos metais de transição. Assim, a equação de Schrödinger, por meio de suas soluções, é a gramática oculta que dita a estrutura de toda a matéria ao nosso redor.

N.B.:
A imagem mental da "nuvem eletrônica" é mais precisa do que a da "partícula em movimento". Um orbital é um mapa de probabilidade instantânea. Se você tirasse uma fotografia ultra-rápida do átomo, veria o elétron em um ponto; ao sobrepor milhões dessas fotografias, veria aparecer a forma do orbital, como um rastro de luz deixado por um dançarino em um palco escuro.