Imagem: Modelo padrão da física de partículas.
As massas das partículas elementares: férmions (caixas verdes), bósons mediadores (caixas amarelas) e bóson de Higgs (caixa vermelha).
Bósons de calibre como fótons e glúons têm massa zero, enquanto todas as outras partículas têm massa, até mesmo o bóson de Higgs, que dá massa às partículas, tem uma massa de cerca de 125,1 GeV/c².
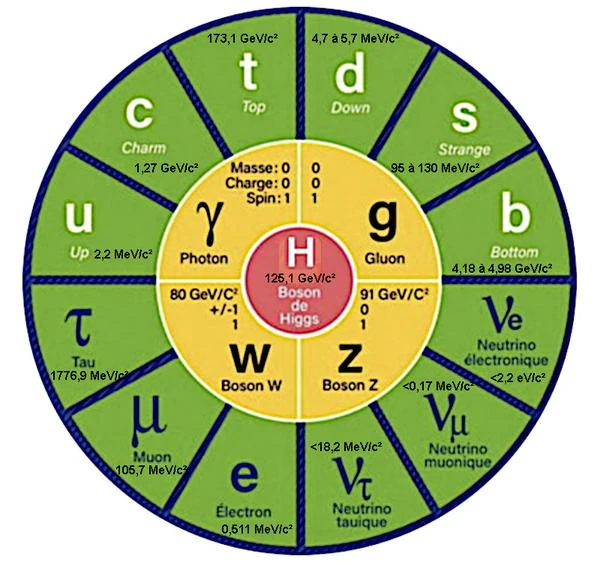
O mundo das partículas elementares e suas interações é descrito pelo que é chamado de Modelo Padrão da física de partículas.
No modelo padrão, algumas partículas elementares como fótons e glúons são consideradas partículas sem massa. Mas para outras partículas, como quarks, bósons W e Z ou léptons, uma massa é medida experimentalmente. A massa, que pode ser convertida em energia e vice-versa, é medida em elétron-volts para tornar os resultados mais facilmente comparáveis.
No entanto, o modelo padrão só se aplica a partículas elementares que não possuem massa intrínseca, ou seja, não possuem massa específica de sua natureza. Além disso, essas partículas devem se mover na velocidade da luz.
Essa bela construção da física conseguiu sair desse impasse em 2012 com a descoberta do bóson de Higgs.
De fato, a massa das partículas não é mais uma propriedade intrínseca, mas vem de sua interação com o campo de Higgs. Quanto mais forte a interação com o campo de Higgs, maior a inércia, o que lhes dá o que chamamos de massa.
A teoria especial da relatividade de Albert Einstein (1879-1955) diz que energia e massa são equivalentes e estão relacionadas pela equação E=mc2.
O que significa que um corpo maciço tem energia só porque tem massa e essa energia é enorme, 1 grama de matéria = 8,99 x 10¹² joules (J).
No que diz respeito às partículas, esta energia representa a massa de uma partícula em repouso. Porém, quando a partícula está em movimento, esta equação deve levar em conta a energia cinética.
E=mc² só apareceu em 1912. Em 1905, a energia total é formulada da seguinte forma E² = m²c⁴ + p²c², se o impulso (p) for nulo então as duas equações são idênticas. A equação também pode ser expressa como: E = √(m²c⁴ + p²c²)
Esta equação E² = (pc)² + (mc²)², ou seu equivalente E = √(m²c⁴ + p²c²), leva em conta a energia da massa e a energia do movimento da partícula.
É precisamente esta fórmula que torna possível a existência de partículas de massa zero. De fato, se seu momento for diferente de zero, a partícula pode não ter massa e ainda ter energia. Nesse caso, as partículas sem massa não podem estar em repouso, elas devem ter uma velocidade, a da luz.
Se um corpo está parado, sua energia total é E=mc². Nesse caso, medimos a inércia de um corpo (massa inercial) como sendo sua massa total. O que significa que sua massa inercial = E/c².
Se um corpo está em movimento, sua energia total é E = √(m²c⁴ + p²c²), ou seja, E = mc² + pc (sua energia cinética).
Assim, para uma partícula sem massa E² = (mc²)² + (pc)² ou E = mc² + pc ou E = pc
Na equação E = mc² + pc, pc representa a energia de movimento de uma partícula. p é o momento da partícula, que é igual à sua massa m multiplicada por sua velocidade v, e c é a velocidade da luz. Assim, pc = mvc, onde m é a massa da partícula e v é a sua velocidade.
Para uma partícula sem massa E = c, é por isso que uma partícula sem massa só pode ter uma velocidade que a da luz.
A inércia é a energia necessária para colocar um corpo estacionário em movimento ou para alterar sua velocidade quando está em movimento. De fato, quanto mais massivo é um corpo, mais ele resiste à mudança de movimento. Em outras palavras, quanto mais massivo for um objeto, mais difícil será acelerá-lo ou desacelerá-lo porque a inércia aumenta com a velocidade. Chega um momento em que a inércia é tão grande que atingimos um limite de velocidade, o da luz.
Teoria do muro de Planck