Última actualización 07 de abril 2023

Las ecuaciones de Maxwell

Las 4 ecuaciones de Maxwell

Maxwell publicó por primera vez en 1865 su teoría en forma de veinte ecuaciones con veinte incógnitas, luego en 1873 reescribió su teoría en forma de ocho ecuaciones. No fue hasta 1884 que Oliver Heaviside (1850-1925) reformuló estas ecuaciones en la forma de cuatro ecuaciones vectoriales y escalares.

Las ecuaciones de Maxwell son, por tanto, un conjunto de cuatro ecuaciones matemáticas que describen las propiedades fundamentales de los campos electromagnéticos, esenciales para comprender la electricidad y el magnetismo.
El campo eléctrico E⃗ es creado por partículas denominadas ρ.
El campo magnético B⃗ es creado por corrientes, es decir, cargas en movimiento, denominadas J. Cuando una corriente pasa a través de un alambre de cobre, se crea un campo magnético (esta corriente desvía la aguja de una brújula colocada cerca).
Muchos fenómenos son tanto eléctricos como magnéticos (ondas que incluyen luz, electrostática, baterías, inducción electromagnética, electroimanes, etc.)

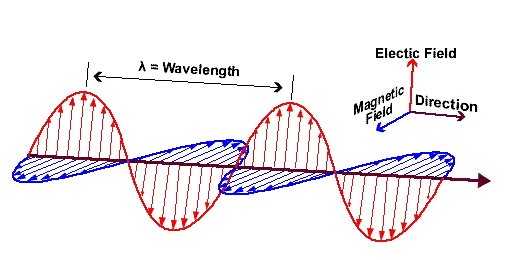
Las ecuaciones de Maxwell a menudo se escriben en notación vectorial para representar campos electromagnéticos (E⃗ y B⃗).

• La primera ecuación de Maxwell, también llamada ley de Gauss, describe cómo pasa el flujo eléctrico a través de una superficie cerrada.
∇.E = ρ/ε0
∇.E es la divergencia del campo eléctrico, que mide la cantidad de flujo eléctrico que sale de una superficie dada.
ρ es la densidad de carga eléctrica en la región considerada y ε0 es la permitividad del vacío, que es una constante física.

• La segunda ecuación de Maxwell, también llamada ley de Gauss para el magnetismo, establece que el flujo magnético total que pasa a través de una superficie gaussiana cerrada es siempre cero.
∇.B=0
∇.B es la divergencia del campo magnético, que mide la cantidad de flujo magnético que sale de una superficie dada.

• La tercera ecuación de Maxwell, también llamada ley de Faraday, describe cómo un campo magnético en movimiento puede crear un campo eléctrico.
∇ x E = -dB/dt
∇ x E es la rotación del campo eléctrico, que mide la circulación del campo eléctrico alrededor de un bucle dado.
dB/dt es la variación temporal del campo magnético.

• La cuarta ecuación de Maxwell, también llamada ley de Ampere-Maxwell, describe cómo un campo eléctrico en movimiento puede crear un campo magnético.
∇ xB = μ0(J + ε0*dE/dt)
∇ x B es la rotación del campo magnético, que mide la circulación del campo magnético alrededor de un bucle dado.
μ0 es la permeabilidad al vacío, que es otra constante física.
J es la densidad de corriente eléctrica en la región considerada y dE/dt es la variación temporal del campo eléctrico.

Las leyes de Maxwell describen el comportamiento de los campos eléctricos y magnéticos y la relación entre los dos. Por lo tanto, las ecuaciones de Maxwell describen cómo los campos eléctricos y magnéticos pueden crearse mutuamente en movimiento.