Descripción de la imagen: La energía solar recibida por una superficie depende del ángulo de incidencia de los rayos solares en relación con esa superficie.
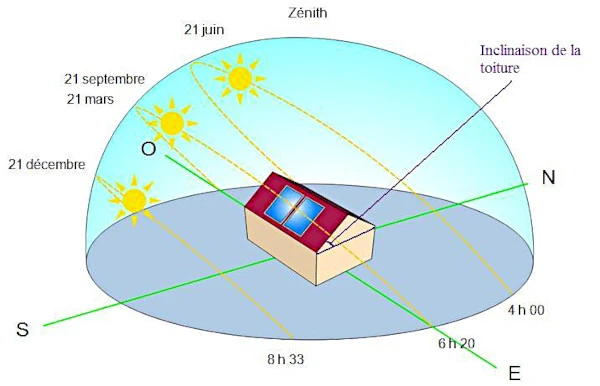
La ley de Lambert (Johann Heinrich Lambert 1728-1777) establece que la intensidad de la energía solar incidente I en una superficie es proporcional al coseno del ángulo de incidencia θ entre el rayo solar y la normal a la superficie: I = I0 cos(θ).
I0 es la intensidad de la energía solar cuando es perpendicular a la superficie, es decir, la intensidad luminosa en vatios por metro cuadrado (W/m²).
El coseno de un ángulo en un triángulo rectángulo es la relación entre la longitud del lado adyacente al ángulo y la longitud de la hipotenusa.
θ es el ángulo de incidencia en relación con la superficie de la Tierra. El ángulo de incidencia está determinado por la posición relativa del Sol respecto a la superficie en cuestión. En general, este ángulo varía en función de la latitud, el día del año y la hora del día. Para una superficie horizontal, el ángulo de incidencia también está influenciado por el ángulo de altura solar (altitud solar) y el acimut solar.
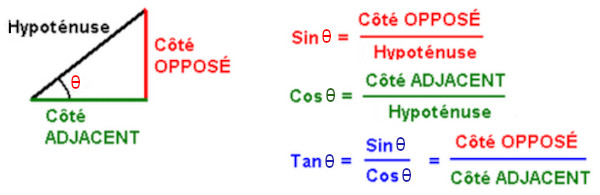
Para una superficie plana inclinada, la energía solar recibida se puede calcular integrando la intensidad de la energía solar sobre la superficie. Si E es la energía en julios (J) recibida por unidad de superficie: E = E0 cos(θ) (E0 es la energía recibida por unidad de superficie cuando los rayos son perpendiculares).
La relación entre la energía E y la intensidad I muestra que la energía total recibida por una superficie es proporcional a la intensidad luminosa, la superficie y el tiempo de exposición.
I = E/A.t
I es la intensidad luminosa en vatios por metro cuadrado (W/m²).
E es la energía en julios (J).
A es la superficie en metros cuadrados (m²).
t es el tiempo en segundos (s).
¿Cuál es la energía solar recibida por una superficie cuando el ángulo de incidencia (con respecto a la vertical), θ = 30 grados?
Intensidad de la energía solar perpendicular a la superficie, I0 = ≈ 1000 W/m², también llamada constante solar (es un valor típico para un cielo despejado al mediodía solar).
I = I0 cos(θ)
cos(30°) = √²/2 ≈ 0.866
I = 1000 W/m² x 0.866 ≈ 866 W/m² o el 86% de la constante solar.
¿Cuál es la energía solar recibida por una superficie cuando el ángulo de incidencia, θ = 45 grados?
I = I0 cos(θ)
cos(45°) = √²/2 ≈ 0.707
I = 1000 W/m² x 0.707 ≈ 707 W/m² o el 70% de la constante solar.
¿Cuál es la energía solar recibida por una superficie cuando el ángulo de incidencia, θ = 90 grados?
I = I0 cos(θ)
cos(90°) = 0
I = 1000 W/m² x 0 ≈ 0 W/m².
• A 30 grados, la superficie recibe ≈ 866 W/m².
• A 45 grados, la superficie recibe ≈ 707 W/m².
• A 66 grados, la superficie recibe ≈ 406 W/m².
• A 90 grados, la superficie recibe 0 W/m².
La segunda ecuación esencial en física
La primera ecuación esencial en física
La fuerza electromagnética o fuerza de Lorentz
¿Por qué el mármol es más frío que la madera?
Teoría del muro de Planck