Description de l'image : L'énergie solaire reçue par une surface dépend de l'angle d'incidence des rayons solaires par rapport à cette surface.
La loi de Lambert (Johann Heinrich Lambert 1728-1777) stipule que l'intensité de l'énergie solaire incidente I sur une surface est proportionnelle au cosinus de l'angle d'incidence θ entre le rayon solaire et la normale à la surface : I = I0 cos(θ)
I0 est l'intensité de l'énergie solaire lorsqu'elle est perpendiculaire à la surface, c'est-à-dire l'intensité lumineuse en watts par mètre carré (W/m²).
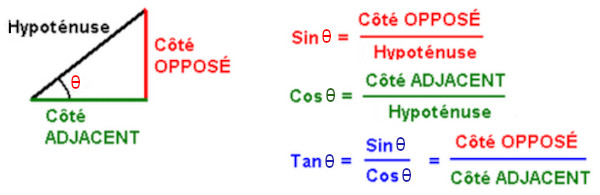
Le cosinus d'un angle dans un triangle rectangle est le rapport entre la longueur du côté adjacent à l'angle et la longueur de l'hypoténuse.
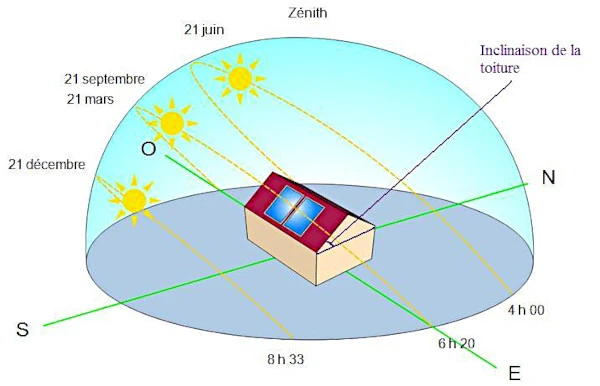
θ est l'angle d'incidence par rapport à la surface de la Terre. L'angle d'incidence est déterminé par la position relative du Soleil par rapport à la surface en question. En général, cet angle varie en fonction de la latitude, du jour de l'année, et de l'heure de la journée. Pour une surface horizontale, l'angle d'incidence est également influencé par l'angle de hauteur solaire (altitude solaire) et l'azimut solaire.
Pour une surface plane inclinée, l'énergie solaire reçue peut être calculée en intégrant l'intensité de l'énergie solaire sur la surface. Si E est l'énergie en joules (J) reçue par unité de surface : E = E0 cos(θ) (E0 est l'énergie reçue par unité de surface lorsque les rayons sont perpendiculaires).
La relation entre l'énergie E et l'intensité I montre que l'énergie totale reçue par une surface est proportionnelle à l'intensité lumineuse, à la surface et au temps d'exposition.
I = E/A.t
I est l'intensité lumineuse en watts par mètre carré (W/m²).
E est l'énergie en joules (J).
A est la surface en mètres carrés (m²).
t est le temps en secondes (s).
Quelle est l'énergie solaire reçue par une surface lorsque l'angle d'incidence (par rapport à la vertical), θ = 30 degrés ?
Intensité de l'énergie solaire perpendiculaire à la surface, I0 = ≈ 1000 W/m², également appelée constante solaire (c'est une valeur typique pour un ciel dégagé à midi solaire).
I = I0 cos(θ)
cos(30°) = √²/2 ≈ 0.866
I = 1000 W/m² x 0.866 ≈ 866 W/m² soit 86% de la constante solaire.
Quelle est l'énergie solaire reçue par une surface lorsque l'angle d'incidence, θ = 45 degrés ?
I = I0 cos(θ)
cos(45°) = √²/2 ≈ 0.707
I = 1000 W/m² x 0.707 ≈ 707 W/m² soit 70% de la constante solaire.
Quelle est l'énergie solaire reçue par une surface lorsque l'angle d'incidence, θ = 90 degrés ?
I = I0 cos(θ)
cos(90°) = 0
I = 1000 W/m² x 0 ≈ 0 W/m².
• À 30 degrés, la surface reçoit ≈ 866 W/m².
• À 45 degrés, la surface reçoit ≈ 707 W/m².
• À 66 degrés, la surface reçoit ≈ 406 W/m².
• À 90 degrés, la surface reçoit 0 W/m².
Rapport entre masse grave et masse inertielle et principe d'équivalence 
La troisième équation essentielle en physique 
La deuxième équation essentielle en physique 
La première équation essentielle en physique 
La force électromagnétique ou force de Lorentz 
Pourquoi le marbre est plus froid que le bois ? 
Théorie du mur de Planck