Un Panneau Photovoltaïque connecté à l’installation domestique (et au réseau fournisseur) produit une tension continue (DC), qui est ensuite convertie en tension alternative synchronisée (AC) par un onduleur. Cette tension est calée sur la même fréquence (50 Hz) et une amplitude comparable à celle du réseau.
En électricité, le courant circule si et seulement s’il existe une différence de potentiel (ΔV) — en particulier en courant continu, où seule la différence de tension instantanée détermine l’écoulement du courant. En revanche, dans le cas de deux sources alternatives synchronisées (même fréquence, même forme d’onde), le courant peut circuler même si les tensions instantanées sont égales par moments, grâce à un déphasage (quelques degrés) entre les sinusoïdes.
Dans ce contexte, c’est la différence de phase entre les tensions, ainsi que les caractéristiques d’impédance du circuit, qui déterminent l’existence et le sens du courant.
N.B. : Dans une tension alternative de 220 V, la tension varie de +311 V à -311 V. En effet, la valeur de 220 V est la valeur efficace (RMS) de la tension alternative. C'est la valeur utilisée pour les calculs de puissance et les spécifications des appareils électriques. La tension alternative oscille entre une valeur positive maximale et une valeur négative maximale. La valeur maximale (amplitude) est en réalité \( V_{\mathrm{CRETE}} = V_{\mathrm{RMS}} \times \sqrt{2} \) → \( 220 \times \sqrt{2} \approx 311\,\text{V} \)
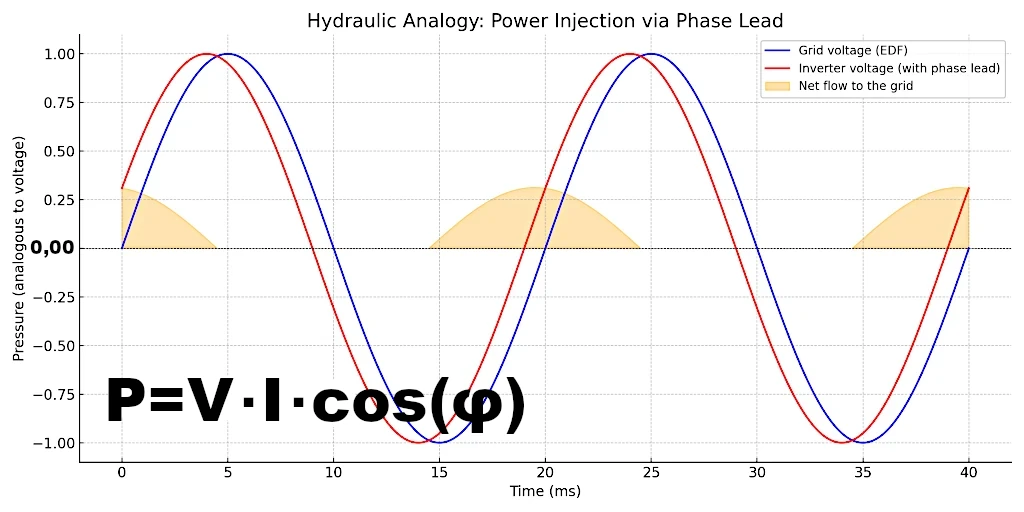
En termes de physique, ce transfert obéit à l’équation de puissance : \( P = V \cdot I \cdot \cos(\varphi) \). Cette formule est connue sous le nom de "Formule de la puissance active en courant alternatif monophasé sinusoïdal".
Même si la tension efficace est nominalement la même (230 V par exemple), ce sont les variations instantanées de tension (phasage, dynamique, micro-ajustements) qui permettent à l’onduleur d’injecter un courant dirigé vers le réseau.
Imaginez deux pompes hydrauliques reliées aux deux extrémités d'un même tuyau, chacune produisant une variation de pression à une fréquence de 50 Hz.
Ces variations créent des ondes de pression dans le fluide (semblables à des ondes sonores) qui se déplacent dans le tuyau. Ces ondes provoquent des zones de compression et de détente du fluide, sans déplacement global de masse, mais avec des oscillations locales des particules d'eau.
Ce système est une bonne analogie avec deux sources de tension alternative dans un circuit électrique : la pression représente la tension, le débit correspond au courant, et la résistance au débit est similaire à l'impédance électrique.
Les deux pressions sont identiques à chaque instant.
Il n’y a aucune différence de pression entre les deux extrémités du tuyau commun.
Donc : débit nul en tout temps, pas de mouvement du fluide.
Conclusion : Aucun transfert d’énergie. Le fluide est statique malgré la pression oscillante.
Pressions opposées : quand l’une pousse, l’autre aspire.
Différence de pression maximale à chaque instant.
Le fluide oscille fortement d’une pompe vers l’autre, en alternance.
Le débit \( Q(t) \) est en opposition de phase avec la différence de pression.
Le produit \( \Delta p(t) \cdot Q(t) \) est négatif la moitié du temps, positif l’autre moitié, mais parfaitement symétrique.
Conclusion :
Quand une pompe est à sa pression maximale, l’autre est au point de débit maximal (car le gradient de pression est en train de changer).
Pression et débit sont en quadrature (90° de décalage).
Cela correspond à une situation où la puissance instantanée est toujours non nulle, mais change de signe au cours du cycle.
Conclusion :
Dans ce cas, le déphasage n'est ni totalement nul (comme dans le cas 0°), ni de 90° (où pression et débit sont en décalage maximal mais sans transfert net), ni maximal (comme dans le cas 180°), mais intermédiaire.
La différence de pression n’est pas maximale en permanence, mais elle varie de manière partielle.
Le débit est également sinusoïdal, mais il est partiellement en phase avec la pression.
Ce déphasage crée un transfert net d'énergie entre les pompes, résultant en un flux réel de fluide d'une pompe à l'autre.
| Cas n° | Déphasage (°) | Différence de pression | Débit \( Q(t) \) | Puissance instantanée | Puissance moyenne |
|---|---|---|---|---|---|
| 1 | 0° | Nulle | Nul | \( P(t) = 0 \) | 0 (aucun transfert) |
| 2 | 90° | Maximale | En quadrature avec la pression | Sinusoïdale, alternance de signes | 0 (transfert réciproque) |
| 3 | 180° | Maximale | Opposé à la pression | Sinusoïdale symétrique | 0 (transfert réciproque) |
| 4 | Intermédiaire (ex : 5°) | Partielle mais non nulle | Partiellement en phase avec la pression | Sinusoïdale, valeur moyenne non nulle | ≠ 0 (transfert net d’énergie) |
Bien qu’un débit instantané alternatif existe dans tous les cas, un transfert net de masse n’apparaît que si le déphasage est partiel (différent de 0°, 90° ou 180°).
Le fluide est donc le support de l’énergie mécanique, et peut devenir un vecteur de transport de matière dans les situations de transfert net d’énergie.
Dynamique de la Quantité de Mouvement pour expliquer la propulsion des fusées ou des méduses 
Distribution énergétique des électrons dans les atomes 
Principe d'incertitude de Heisenberg : Comprendre l'incertitude quantique 
Relation entre Energie, Puissance et Temps 
Pourquoi y a-t-il une limite au froid, mais pas au chaud ? 
La loi de la chute des corps de Galilée 
La Loi des gaz parfaits 
Équation de Schrödinger et Structure des Atomes 
Théorème de Noether : la conservation de l'énergie découle des symétries 
Rapport entre masse grave
et masse inertielle et principe d'équivalence 
La troisième
équation essentielle en physique 
La deuxième équation
essentielle en physique 
La première équation
essentielle en physique 
La force électromagnétique ou force de Lorentz
L'énergie solaire reçue varie en fonction
de l'inclinaison 
Pourquoi le marbre est plus froid que le bois ? 
Théorie du mur de Planck