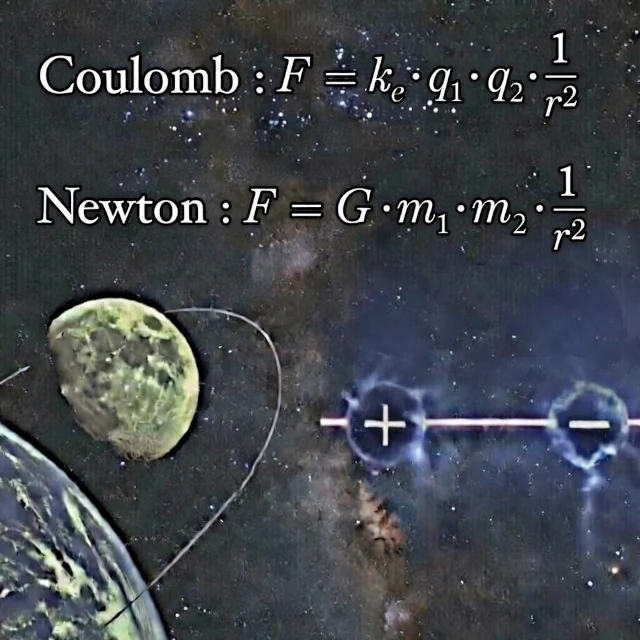
Pourquoi la Lune tourne-t-elle autour de la Terre ? Pourquoi vos cheveux se dressent-ils après avoir retiré un bonnet en laine ? La réponse à ces deux questions, pourtant si différentes, s'écrit avec une structure mathématique presque identique. D'un côté, la loi de la gravitation universelle formulée par Isaac Newton (1643-1727) à la fin du 17e siècle. De l'autre, la loi de l'électrostatique établie par Charles-Augustin de Coulomb (1736-1806) à la fin du 18e siècle. Toutes deux sont des « lois en carré inverse de la distance ».
Pour la gravité : \( F_g = G \cdot \frac{m_1 \cdot m_2}{r^2} \)
Pour l'électricité : \( F_e = k_e \cdot \frac{q_1 \cdot q_2}{r^2} \)
Dans ces équations, \( F \) représente la force, \( m \) la masse, \( q \) la charge électrique et \( r \) la distance entre les deux objets. Les constantes \( G \) et \( k_e \) ne sont que des facteurs d'échelle. Cette similarité frappante est-elle une coïncidence cosmique ou le signe d'une vérité plus profonde sur la structure de l'Univers ?
La raison la plus fondamentale de cette similitude est géométrique.
Nous vivons dans un espace à trois dimensions. Imaginez une source ponctuelle d'influence, qu'il s'agisse d'une masse ou d'une charge. Cette influence se propage de manière sphérique et isotrope (identique dans toutes les directions) autour d'elle.
À une distance \( r \) de la source, toute l'influence émise doit traverser une surface sphérique imaginaire. Pourquoi une surface et pas un volume ? Parce que l'influence se propage comme un front d'onde sphérique. À un instant donné, tous les points situés à la même distance \( r \) de la source sont atteints simultanément. Ces points forment précisément une surface sphérique, pas un volume.
La surface d'une sphère est donnée par la formule \( 4\pi r^2 \). L'énergie ou l'intensité de l'effet (qu'on appelle le flux) se répartit donc uniformément sur cette surface à mesure qu'elle s'éloigne de la source.
Si la source émet une quantité totale d'influence par seconde que nous appellerons \( Q \) (un débit), alors l'intensité \( I \) que l'on mesure en un point situé à la distance \( r \) est cette quantité totale divisée par la surface sur laquelle elle s'étale : \( I = \frac{Q}{4\pi r^2} \)
Cette expression signifie que plus on s'éloigne, plus la surface à traverser est grande (\( 4\pi r^2 \) augmente avec \( r \)), donc plus l'intensité par unité de surface diminue. C'est exactement comme la lumière d'une bougie : à 1 mètre, elle éclaire une certaine surface ; à 2 mètres, la même quantité de lumière doit éclairer une surface 4 fois plus grande (car \( (2)^2 = 4 \)), donc l'intensité lumineuse par unité de surface est 4 fois plus faible.
Le volume n'intervient pas ici car nous mesurons un effet en un point de la surface, pas dans un espace tridimensionnel. La grandeur physique pertinente est la densité surfacique de flux, pas une densité volumique.
Cette expression se décompose en deux parties :
- \( Q \) est une constante qui dépend uniquement de la source (sa puissance d'émission).
- \( \frac{1}{4\pi r^2} \) est un facteur géométrique qui décrit comment l'influence se dilue sur une surface sphérique.
Mathématiquement, on peut réécrire : \( I = \left( \frac{Q}{4\pi} \right) \times \frac{1}{r^2} \)
Le terme \( \frac{Q}{4\pi} \) est une constante globale pour une source donnée. La dépendance en fonction de la distance est donc entièrement contenue dans le facteur \( \frac{1}{r^2} \). C'est pourquoi on dit que l'intensité est inversement proportionnelle au carré de la distance.
Dans les lois de Coulomb et de Newton, on retrouve cette même structure :
- Pour Coulomb : \( F = k_e \cdot q_1 \cdot q_2 \cdot \frac{1}{r^2} \)
- Pour Newton : \( F = G \cdot m_1 \cdot m_2 \cdot \frac{1}{r^2} \)
Les constantes \( k_e \) et \( G \) intègrent déjà les facteurs géométriques comme \( \frac{1}{4\pi} \) (dans le système d'unités adapté, comme le système SI rationalisé), ainsi que les propriétés fondamentales de l'interaction.
Si nous vivions dans un univers à deux dimensions, l'influence se répartirait sur un cercle (un périmètre) de longueur \( 2\pi r \), et la loi deviendrait \( I = \frac{Q}{2\pi r} = \left( \frac{Q}{2\pi} \right) \times \frac{1}{r} \), soit une loi en \( 1/r \). À quatre dimensions, elle suivrait une loi en \( 1/r^3 \). La loi en carré inverse est donc la signature mathématique d'une force qui se propage dans un espace à trois dimensions.
Si la forme mathématique est identique, la nature profonde de ces deux forces est radicalement différente. La première différence saute aux yeux : la masse est toujours positive, la gravité est donc toujours attractive. Les charges électriques, en revanche, peuvent être positives ou négatives. L'interaction électrique peut donc être aussi bien attractive que répulsive.
Ainsi, la loi de Coulomb a deux visages complémentaires qui structurent notre réalité :
C'est cette dualité qui fait de la loi de Coulomb l'un des piliers les plus élégants et les plus fondamentaux de la physique. Sans elle, l'Univers ne serait qu'une soupe de particules indifférenciées, sans structure, sans vie, et sans table sur laquelle poser votre main.
La seconde différence réside dans l'intensité. La force électrique est colossalement plus puissante que la force gravitationnelle. Pour vous en convaincre, comparez la force électrique de répulsion entre deux protons et leur force d'attraction gravitationnelle. Le rapport est d'environ \( 10^{36} \) en faveur de l'électricité. Si la gravité domine à l'échelle des planètes et des galaxies, c'est uniquement parce que la matière est électriquement neutre à grande échelle. Les charges positives et négatives s'annulent, ne laissant que la faible mais omniprésente gravité.
| Propriété | Gravitation (Newton) | Électrostatique (Coulomb) |
|---|---|---|
| Source | Masse (toujours positive) | Charge électrique (positive ou négative) |
| Nature de la force | Toujours attractive | Attractive ou répulsive |
| Constante | \( G = 6,674 \times 10^{-11} \, \text{N·m}^2/\text{kg}^2 \) | \( k_e = 8,988 \times 10^9 \, \text{N·m}^2/\text{C}^2 \) |
| Intensité relative | \( 10^{-36} \) (la plus faible) | \( 10^{36} \) (beaucoup plus forte) |
| Écrantage | Impossible (pas de masse négative) | Possible (neutralité électrique) |
| Domaine de prédominance | Astronomique (planètes, galaxies) | Atomique et moléculaire |
Cette ressemblance a fasciné les plus grands esprits. Albert Einstein (1879-1955) a passé les trente dernières années de sa vie à tenter d'unifier la gravité et l'électromagnétisme dans une seule et même théorie, une "théorie du champ unifié". Il a échoué, mais sa quête a ouvert la voie à la physique moderne. Aujourd'hui, nous savons que ces deux forces sont les manifestations, à basse énergie, de théories plus profondes.
La gravité est décrite par la relativité générale comme une courbure de l'espace-temps. L'électromagnétisme, dont l'électrostatique fait partie, est décrit par l'électrodynamique quantique. L'unification de ces deux piliers (la relativité générale et la mécanique quantique) reste le Saint-Graal de la physique théorique, une quête pour comprendre pourquoi, à un niveau fondamental, ces deux forces si différentes partagent cette élégante structure mathématique.
L'équation de Kaya : L'équation qui complique notre décarbonation 
La vitesse indépassable dans l’Univers : quand l'énergie devient infinie 
L’emballement électromagnétique : Le secret de la Vitesse de la lumière 
Comprendre l'Effet Photoélectrique : La Lumière et les Électrons 
À quelle distance se trouve l’horizon ? 
Comment les Panneaux
Solaires Injectent-ils l'Électricité dans le Réseau ? 
Dynamique de la Quantité de Mouvement pour expliquer
la propulsion des fusées ou des méduses 
Comment l'énergie des électrons dicte les propriétés chimiques 
Le rôle clé du principe d'incertitude quantique : Aucune particule ne peut être immobile 
Énergie et puissance : Ne pas confondre, le temps fait toute la différence 
Pourquoi y a-t-il une limite au froid, mais pas au chaud ? 
La loi de la chute des corps de Galilée 
La Loi des gaz parfaits : Une équation, des milliers d'applications 
L'équation de Schrödinger a révolutionné notre vision de la matière 
La magie du théorème de Noether : Du principe de moindre action aux lois de conservation 
Rapport entre masse grave et masse inertielle et principe d'équivalence
Troisième Equation de la Physique : La quantité de mouvement pour comprendre les collisions 
La deuxième équation essentielle en physique : L'intuition d'une grandeur qui se conserve 
La première équation de la physique : Comment mathématiser la force 
La force électromagnétique ou force de Lorentz 
L'énergie solaire reçue varie en fonction de l'inclinaison 
Pourquoi le marbre est plus froid
que le bois ? 
Pourquoi
un photon, qui n'a pas de masse, a une énergie ? 
Formule de Bayes et Intelligences Artificielles 
Les sept constantes fondamentales
de la physique 
Quelle est la température ressentie dans l'espace interstellaire ?
Courbes de rayonnement du corps noir : la loi de Planck
Le principe d'équivalence, les effets gravitationnels sont indiscernables d'une
accélération 
E=mc2 : Les quatre concepts fondamentaux de l'univers revisités 
Comment peser le soleil ? 
Equation de la chute libre des corps (1604) 
Coulomb vs Newton : la mystérieuse similitude des forces de l'Univers 
Equation de Boltzmann sur l'entropie (1877) 
Les équations de la relativité restreinte (1905)
L'équation de la relativité générale (1915) 
Équations de la rotation planétaire : entre moment cinétique et équilibre gravitationnel
Équation de la vitesse orbitale d'une planète 
L'équation de Planck 
Comprendre l'équation de Schrödinger sans faire de maths 
Les trois lois de Newton : De la pomme qui tombe aux planètes qui tournent 
Les équations de Maxwell 
Equation de Dirac 
Conservation de l'énergie 
Equation de l'induction électromagnétique 
Pourquoi les particules élémentaires n'ont pas de masse ? 
Différences entre chaleur et température