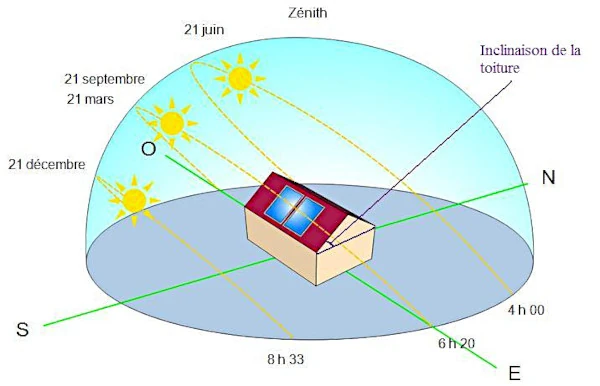
Description of the image: The solar energy received by a surface depends on the angle of incidence of the solar rays relative to that surface.
Lambert's law (Johann Heinrich Lambert 1728-1777) states that the intensity of the incident solar energy I on a surface is proportional to the cosine of the angle of incidence θ between the solar ray and the normal to the surface: I = I0 cos(θ).
I0 is the intensity of the solar energy when it is perpendicular to the surface, that is, the luminous intensity in watts per square meter (W/m²).
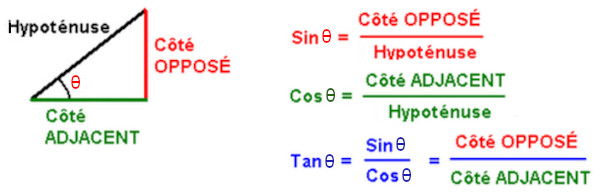
The cosine of an angle in a right triangle is the ratio of the length of the adjacent side to the length of the hypotenuse.
θ is the angle of incidence relative to the Earth's surface. The angle of incidence is determined by the relative position of the Sun to the surface in question. In general, this angle varies depending on latitude, the day of the year, and the time of day. For a horizontal surface, the angle of incidence is also influenced by the solar altitude angle and the solar azimuth.
For an inclined flat surface, the solar energy received can be calculated by integrating the intensity of the solar energy over the surface. If E is the energy in joules (J) received per unit area: E = E0 cos(θ) (E0 is the energy received per unit area when the rays are perpendicular).
The relationship between energy E and intensity I shows that the total energy received by a surface is proportional to the luminous intensity, the area, and the exposure time.
I = E/A.t
I is the luminous intensity in watts per square meter (W/m²).
E is the energy in joules (J).
A is the area in square meters (m²).
t is the time in seconds (s).
What is the solar energy received by a surface when the angle of incidence (relative to the vertical), θ = 30 degrees?
Intensity of the solar energy perpendicular to the surface, I0 = ≈ 1000 W/m², also called the solar constant (this is a typical value for a clear sky at solar noon).
I = I0 cos(θ)
cos(30°) = √²/2 ≈ 0.866
I = 1000 W/m² x 0.866 ≈ 866 W/m² or 86% of the solar constant.
What is the solar energy received by a surface when the angle of incidence, θ = 45 degrees?
I = I0 cos(θ)
cos(45°) = √²/2 ≈ 0.707
I = 1000 W/m² x 0.707 ≈ 707 W/m² or 70% of the solar constant.
What is the solar energy received by a surface when the angle of incidence, θ = 90 degrees?
I = I0 cos(θ)
cos(90°) = 0
I = 1000 W/m² x 0 ≈ 0 W/m².
• At 30 degrees, the surface receives ≈ 866 W/m².
• At 45 degrees, the surface receives ≈ 707 W/m².
• At 66 degrees, the surface receives ≈ 406 W/m².
• At 90 degrees, the surface receives 0 W/m².
The Second Essential Equation in Physics
The first essential equation in physics
The electromagnetic force or Lorentz force
Why is marble colder than wood?
Planck's wall theory