Description of the image: Portrait of Amalie Emmy Noether (1882-1935), German mathematician. Noether's theorem states that the laws of physics are symmetric, and this symmetry leads to conservation laws. Image source: public domain.
Statement of Noether's Theorem: "To every infinitesimal transformation that leaves the action integral invariant corresponds a conserved quantity."
Noether's theorem, proved in 1915 and published in 1918, is a fundamental concept in theoretical physics that establishes a deep connection between conservation laws and the symmetries of physical systems.
In other words, "If a physical law remains the same even after a small transformation (such as a displacement in space or a change in time), then there exists a quantity that does not change over time, i.e., a conserved quantity (energy, momentum, charge, etc.)."
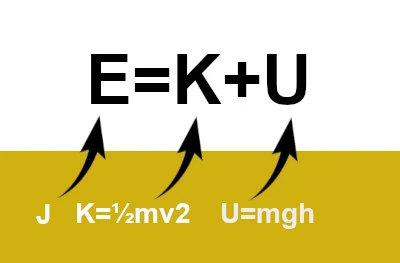
Example of the pendulum: the total mechanical energy E of the simple pendulum can be expressed as the sum of its kinetic energy (K) and potential energy (U) E=K+U.
The kinetic energy K of the pendulum is given by: K=½mv2 where m is the mass of the pendulum and v is its velocity.
The potential energy U due to gravity is given by: U=mgh where m is the mass of the pendulum, g is the acceleration due to gravity, and h is the height of the pendulum relative to its equilibrium position.
The total mechanical energy E of the pendulum remains constant, meaning that even though the kinetic energy may change depending on the pendulum's velocity, it will be compensated by corresponding changes in the potential energy to keep E constant.
This reflects the conservation of the pendulum's total mechanical energy, in accordance with Noether's theorem.
Note: A conserved quantity is a physical quantity that remains constant over time. For example, energy, momentum (impulse), or angular momentum are conserved quantities.
Symmetries are not just aesthetic; they form the foundation of many fundamental principles in physics. Thanks to Noether's theorem, we know that every symmetry is associated with a conservation law, for example, the conservation of energy, conservation of charge, momentum, and angular momentum.
Symmetry describes the invariances or invariants in the laws of nature. In physics, different types of symmetries are distinguished, and each type has specific implications.
Translation symmetry means that the physical laws remain unchanged when a system is moved in space without rotation. This means that the results of experiments do not depend on the absolute position of objects in space. The results will be the same in Paris, New York, on Earth, on Mars, or anywhere else in the cosmos. If the laws of physics do not change when we move a system by several kilometers or several light-years, this results in the conservation of the system's momentum vector. Thus, translation symmetry implies the conservation of momentum.
Rotation symmetry states that the physical laws are invariant under rotation around a fixed axis. In other words, if we rotate a system around a point, the laws governing its behavior remain the same. For example, when a planet orbits the Sun, its angular momentum remains constant if no external force acts to change its trajectory. Thus, rotation symmetry leads to the conservation of angular momentum.
Time symmetry implies that the laws of physics remain unchanged under a translation in time. This means that the laws were the same in the past, are the same today, and will be the same in millions of years. For example, in the absence of friction and other dissipative forces, the mechanical energy of the pendulum (the sum of kinetic energy and potential energy) remains constant throughout the motion. The kinetic energy (when the pendulum is at its lowest point) and the potential energy (when it is at its highest point) transform into each other, but the total sum remains the same. Thus, the time symmetry of the pendulum is related to the conservation of energy. In a closed system, total energy remains constant over time.
Parity symmetry concerns the invariance of the laws of physics under spatial inversion, meaning that if all the coordinates of a point are inverted with respect to a center: (����,����,����) → (−����,−����,−����). For example, when an electron is directed towards a target made of protons, it interacts with the protons via electromagnetic interaction. If we consider the coordinates of the electron and the proton, the parity transformation involves reversing the positions of the particles. For an electron moving in a given direction, if the sign of its spatial coordinates is changed, the laws governing elastic scattering remain unchanged under this transformation. Thus, parity symmetry leads to the conservation of total energy and total momentum.
Charge symmetry states that the laws of physics remain the same if all charges are reversed. For example, if electrons are replaced by positrons or protons by antiprotons, the results of interactions remain unchanged, and the annihilation process remains the same. Thus, electron-positron annihilation verifies the conservation of charge.
Gauge symmetries are transformations of the fields associated with particles that do not change the laws of physics. Theories of electromagnetism, weak and strong interactions, are all gauge theories. For example, if we modify the potentials associated with a field, gauge symmetry preserves the equations of motion and does not alter physical observables (such as electric and magnetic fields). Thus, gauge symmetries are directly linked to the conservation of electric charge (in quantum electrodynamics), or the conservation of color charge (in quantum chromodynamics).
Before Noether, it was known that certain quantities (such as energy or momentum) were conserved in physical systems, but her theorem revealed that this conservation directly results from the underlying symmetries of the laws of physics.
Conservation laws are cornerstones on which much of modern physics rests. If conservation laws were false, our understanding of the universe, our ability to predict its behavior, and even our technology would collapse, as they are based on these fundamental principles.
Why is there a limit to cold, but not to heat? 
Galileo's Law of Falling Bodies 
The Ideal Gas Law 
Schrödinger Equation and Atomic Structure 
Relationship
between gravitational mass and inertial mass and the equivalence principle 
The Third Essential Equation
in Physics 
The Second Essential Equation
in Physics 
The first essential equation
in physics 
The electromagnetic force or Lorentz force 
The solar energy received depends on
the angle of incidence 
Why is marble colder
than wood? 
Planck's wall theory