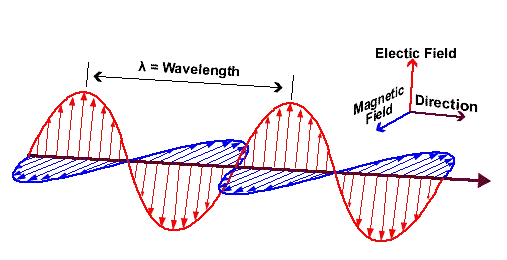
Image: According to the equations of James Clerk Maxwell (1831-1879), light is a self-propagating electromagnetic transverse wave with electric and magnetic components where electric and magnetic fields oscillate at right angles to each other and propagate perpendicular to the direction in which they move indefinitely unless absorbed by the intermediate matter. In other words, each type of field - electric and magnetic - generates the other in order to propagate the entire composite structure in empty space at the finite speed of light.
Maxwell first published in 1865 his theory in the form of twenty equations with twenty unknowns, then in 1873 he rewrote his theory in the form of eight equations. It was not until 1884 that Oliver Heaviside (1850-1925) reformulated these equations in the form of the four vector and scalar equations.
Maxwell's equations are therefore a set of four mathematical equations that describe the fundamental properties of electromagnetic fields, essential in understanding electricity and magnetism.
The electric field E⃗ is created by particles denoted ρ.
The B⃗ magnetic field is created by currents, i.e. charges in motion, denoted J. When a current passes through a copper wire, a magnetic field is created (this current deflects the needle of a compass placed nearby).
Many phenomena are both electrical and magnetic (waves including light, electrostatics, batteries, electromagnetic induction, electromagnets, etc.)
Maxwell's equations are often written in vector notation to represent electromagnetic fields (E⃗ and B⃗).
• Maxwell's first equation, also called Gauss's law, describes how electric flow passes through a closed surface.
∇.E = ρ/ε0
∇.E is the electric field divergence, which measures the amount of electric flux exiting a given surface.
ρ is the electric charge density in the considered region, and ε0 is the vacuum permittivity, which is a physical constant.
• Maxwell's second equation, also called Gauss's law for magnetism, states that the total magnetic flux passing through a closed Gaussian surface is always zero.
∇.B=0
∇.B is the magnetic field divergence, which measures the amount of magnetic flux exiting a given surface.
• Maxwell's third equation, also called Faraday's law, describes how a moving magnetic field can create an electric field.
∇ x E = -dB/dt
∇ x E is the rotational of the electric field, which measures the circulation of the electric field around a given loop.
dB/dt is the temporal variation of the magnetic field.
• Maxwell's fourth equation, also called Ampere-Maxwell's law, describes how a moving electric field can create a magnetic field.
∇ x B = μ0(J + ε0*dE/dt)
∇ x B is the rotational of the magnetic field, which measures the circulation of the magnetic field around a given loop.
μ0 is the vacuum permeability, which is another physical constant.
J is the electric current density in the considered region, and dE/dt is the temporal variation of the electric field.
Maxwell's laws describe the behavior of electric and magnetic fields and the relationship between the two. Thus, Maxwell's equations describe how electric and magnetic fields can create each other in motion.