Relation between Energy, Power, and Time

Image description: Power corresponds to the rate at which energy is transferred or converted. Image source: astronoo.com

What is Energy?

In physics, energy is the capacity of a system to do work, that is, to cause a displacement under the action of a force. It exists in various forms: kinetic, potential, thermal, chemical, electrical, or gravitational.

Power: A Dynamic Concept

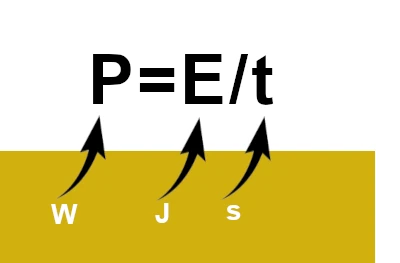
Power corresponds to the rate at which energy is transferred or converted. Mathematically, it is defined by the following relation:

P = E / t or Power = \(\frac{\text{Energy}}{\text{Time}}\)

where P represents power in watts (W), E energy in joules (J), and t time in seconds (s).

Concrete Example: Electric Heating

Consider an electric heater with a power of 1000 W. This means it consumes 1000 J of energy per second. If this heater operates for 1 hour (3600 seconds), the total energy consumed is:

E = P × t = 1000 W × 3600 s = 3,600,000 J (or 1 kWh)

Relationship between Time and Efficiency

The efficiency of electric heating is defined as the ratio of useful energy supplied (heat emitted) to electrical energy consumed:

\(\Large \eta = \frac{E_{\text{useful}}}{E_{\text{consumed}}}\)

In conventional electric heating (resistive), the efficiency is close to 100% (η≈1) because almost all electrical energy is converted into heat.

However, for systems such as heat pumps (HPs), time plays a crucial role in efficiency.

A HP can deliver several times the energy consumed by drawing heat from the air or ground, resulting in a Coefficient of Performance (COP) greater than 1.

For example, if a HP consumes electrical energy of \( E_{\text{consumed}} = 1 \, kWh \) and delivers useful energy of \( E_{\text{useful}} = 3 \, kWh \) in the form of heat, then the Coefficient of Performance is given by:

\[COP = \frac{E_{\text{useful}}}{E_{\text{consumed}}} = \frac{3 \, kWh}{1 \, kWh} = 3\]

In this example, the HP delivers useful energy three times greater than the electrical energy consumed, by capturing freely available heat from the external environment.

ATTENTION: The HP does not "create" energy but transfers heat from an external source (air, water, ground) to the interior. The additional energy comes from capturing this environmental heat.

This example shows how energy, power, and time are intrinsically linked. Understanding these relationships is fundamental in various fields ranging from domestic energy to heavy industry.