Planetary Rotation Equations: Between Angular Momentum and Gravitational Equilibrium

The Planetary Rotation Movement

Examples of Rotational Speeds in the Solar System

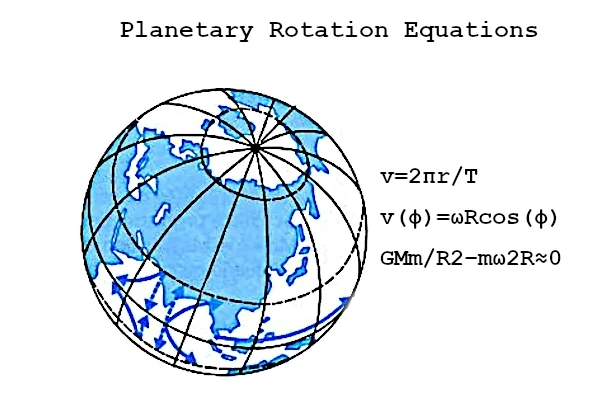
To illustrate this equation, let's take a few characteristic examples from the Solar System. Earth, with an average radius of \(r = 6,371 \text{ km}\) and a rotation period of \(T = 24 \text{ h}\), has an equatorial speed of approximately \(v = \frac{2\pi r}{T} ≈ 1,670 \text{ km/h}\).
The planet Mars, smaller with a radius of \(r = 3,389 \text{ km}\) and a rotation period of \(T = 24 \text{ h } 36 \text{ min}\), rotates more slowly, with its equatorial speed reaching about \(868 \text{ km/h}\) at the Martian equator.

Influence of Radius and Rotation Period

This relationship shows that the rotational speed depends directly on the planet's radius and the duration of its sidereal day. A larger planet or one that rotates faster has a higher rotational speed at the equator. Conversely, a compact or slow planet will have a lower linear speed.

Variation of Speed with Latitude

Finally, it is important to note that this speed is only valid for the equator. As one approaches the poles, the distance to the axis of rotation decreases, and the rotational speed becomes \(v(\phi) = \omega R \cos(\phi)\), where \(\phi\) is the latitude. Thus, although the rotation period remains the same for all points on the globe (24 h for Earth), the linear speed continuously decreases until it becomes zero at the poles.

The Role of Angular Momentum

The rotational motion of a planet around its axis is governed by its angular momentum \(L\), defined by the fundamental relation: \((L = I \omega)\) where \(I\) is the moment of inertia and \(\omega\) is the angular speed. This equation expresses the distribution of mass around the axis and the speed of rotation. A planet in equilibrium retains its angular momentum as long as no external force exerts a torque on it.

Variations and Implications of Rotational Speed

Zero Speed at the Poles

At the North and South Poles, the rotational speed is actually zero, as these points coincide with the Earth's axis of rotation. Thus, although the Earth rotates on itself, the poles remain stationary relative to this axis: they do not describe any circle, unlike points at lower latitudes.

The Evolution of Earth's Rotation Over Time

About 600 million years ago, the Earth's day lasted about 22 hours. This indicates that the Earth was rotating faster than today. The gradual slowdown of the rotation is due to the gravitational interaction with the Moon (a phenomenon known as tidal braking).

The Limits of the Equation \(v = \frac{2\pi r}{T}\)

This simple relationship is not universal. It applies well to solid bodies in uniform rotation, such as terrestrial planets, but not to stars, whose fluid structure causes differential rotation. In other words, the rotation period depends on latitude: equatorial regions rotate faster than polar regions.

Example: The Sun's Differential Rotation

In the case of the Sun, the rotation period varies from about 25 days at the equator to 34 days at the poles. This difference reflects the plasma nature of the Sun, where the layers are not rigid. Its equatorial rotational speed reaches about 2 km/s.

Physical Interest of the Relation \(v = \frac{2\pi r}{T}\)

Knowledge of the rotational speed of a celestial body is essential for understanding its physical characteristics and its dynamic processes. It is directly related to the duration of the sidereal day and provides clues about the internal evolution and history of the planet.

For example, on Jupiter, the extremely rapid rotation (less than 10 hours) generates immense convection cells and giant cyclonic storms, the most famous of which is the Great Red Spot.

The Link Between Gravity and Rotation

Planetary rotation results from a balance between gravitational attraction and centrifugal force. Dynamic equilibrium is achieved when the centrifugal force at the surface partially compensates for gravity: \((\frac{G M m}{R^2} - m \omega^2 R \approx 0)\) where \(G\) is the gravitational constant, \(M\) is the mass of the planet, \(m\) is the mass of a body on the surface, and \(R\) is the planetary radius. This relationship shows that the rapid rotation of a planet tends to reduce the apparent weight at the equator.

Dynamic Consequences and Stability

Planets do not retain their rotational speed forever. Under the effect of tidal forces, their angular momentum can be transferred to their satellite or to their orbit. Thus, the Earth is gradually slowing down, and the Moon is moving away by about 3.8 cm per year. This dissipation of energy tends toward a state of synchronous rotation, as observed between the Moon and the Earth.

Rotational stability also depends on the internal mass distribution. Fluid planets like Jupiter or Saturn exhibit strong flattening due to their high angular speed \((\omega)\), while rocky planets, being more rigid, resist this deformation more.

Origin of Planetary Angular Momentum

During the formation of the protoplanetary disk, collisions and local collapses imposed a preferential rotational motion. The total angular momentum was distributed between the Sun, the planets, and their satellites. This distribution, already analyzed by Isaac Newton (1643-1727) and later formalized by Laplace (1749-1827), explains the almost uniform rotation of planetary bodies around the same ecliptic plane.

Fundamental Equations of Rotation

The linear speed of a point on the surface is defined as: \((v = \omega R)\) and the rotation period \(T\) as: \((\omega = \frac{2\pi}{T})\)
These equations relate observable quantities and allow the calculation of the duration of the planetary day. For example, Jupiter, with a radius \(R = 71,492 \text{ km}\) and \(T = 9.93 \text{ h}\), has an equatorial speed \(v ≈ 12.6 \text{ km/s}\), much higher than that of Earth \((0.465 \text{ km/s})\).

N.B.:
The gyroscopic effects of a rotating planet explain the precession of the equinoxes and the slow variations in the inclination of the axis. These phenomena directly influence the climate over timescales of several thousand years (Milankovitch cycles).

Source: NASA Planetary Fact Sheet, Astronoo.