Planetenrotationsgleichungen: zwischen Drehimpuls und Gravitationsgleichgewicht

Die Planetenrotationsbewegung

Beispiele für Rotationsgeschwindigkeiten im Sonnensystem

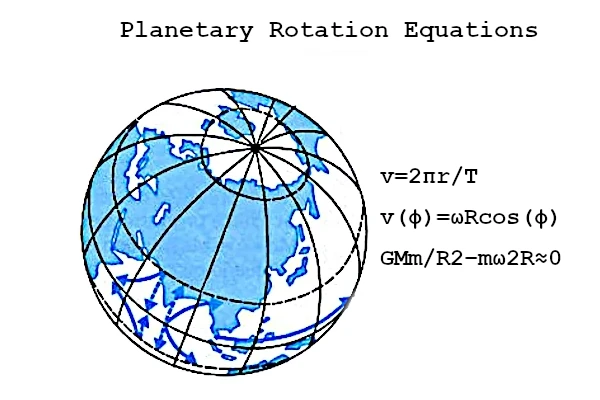
Um diese Gleichung zu veranschaulichen, nehmen wir einige charakteristische BeispieleSonnensystem. DortErde, dessen durchschnittlicher Radius \(r = 6\,371 \text{ km}\) und die Rotationsperiode \(T = 24 \text{ h}\) beträgt, stellt a daräquatoriale Geschwindigkeitvon ca \(v = \frac{2\pi r}{T} ≈ 1\,670 \text{ km/h}\).
Der PlanetMarsch, kleiner mit einem Radius von \(r = 3\,389 \text{ km}\) und einer Rotationsperiode von \(T = 24 \text{ h } 36 \text{ min}\), rotiert langsamer, seine Äquatorgeschwindigkeit erreicht am Marsäquator etwa \(868 \text{ km/h}\).

Einfluss von Radius und Rotationsperiode

Dieser Zusammenhang zeigt, dass die Rotationsgeschwindigkeit direkt vom Radius des Planeten und der Länge seines Sterntages abhängt. Ein größerer oder schneller rotierender Planet hat am Äquator eine höhere Rotationsgeschwindigkeit. Umgekehrt hat ein kompakter oder sich langsam bewegender Planet eine geringere Lineargeschwindigkeit.

Variation der Geschwindigkeit mit dem Breitengrad

Abschließend ist zu beachten, dass diese Geschwindigkeit nur für den Äquator gilt. Wenn wir uns den Polen nähern, verringert sich der Abstand von der Rotationsachse und die Rotationsgeschwindigkeit wird \(v(\phi) = \omega R \cos(\phi)\), wobei \(\phi\) der Breitengrad ist. Obwohl also die Rotationsperiode für alle Punkte auf dem Globus gleich bleibt (24 Stunden für die Erde), Die Lineargeschwindigkeit nimmt kontinuierlich ab, bis sie an den Polen Null wird.

Die Rolle des Drehimpulses

Die Rotationsbewegung eines Planeten um seine Achse wird durch seine bestimmtDrehimpuls\(L\), definiert durch die grundlegende Beziehung: \((L = I \omega)\) wobei \(I\) das istTrägheitsmomentund \(\omega\) dieWinkelgeschwindigkeit. Diese Gleichung drückt die Massenverteilung um die Achse und die Rotationsgeschwindigkeit aus. Ein im Gleichgewicht befindlicher Planet behält seinen Drehimpuls, solange keine äußere Kraft ein Drehmoment auf ihn ausübt.

Drehzahlschwankungen und Auswirkungen

Nullgeschwindigkeit an den Polen

ZuNord- und Südpol, DortRotationsgeschwindigkeitist eigentlich Null, weil diese Punkte mit dem zusammenfallenRotationsachse der Erde. Obwohl sich die Erde also um ihre Achse dreht, bleiben die Pole in Bezug auf diese Achse stationär: Sie beschreiben keinen Kreis, im Gegensatz zu Punkten in niedrigeren Breiten.

Die Entwicklung der Erdrotation im Laufe der Zeit

Es gibt ungefähr600 Millionen Jahre, DortTag der Erdedauerte ca22 Uhr. Dies deutet darauf hin, dass sich die Erde schneller drehte als heute. Die fortschreitende Verlangsamung der Rotation ist darauf zurückzuführenGravitationswechselwirkung mit dem Mond(ein Phänomen, bekannt alsGezeitenbremsung).

Die Grenzen der Gleichung \(v = \frac{2\pi r}{T}\)

Diese einfache Beziehung ist nicht universell. Es gilt gut fürfeste Körperin gleichmäßiger Rotation, wie die tellurischen Planeten, aber nichtSterne, dessen Fluidstruktur eine Rotation erzeugtDifferential. Mit anderen Worten, dieRotationsperiodehängt vom Breitengrad ab: Äquatorregionen rotieren schneller als Polarzonen.

Beispiel: die unterschiedliche Rotation der Sonne

Im Fall vonSonne, die Rotationsperiode variiert von ungefähr25 Tage bis zum Äquatorhat34 Tage an den Polen. Dieser Unterschied spiegelt die Natur widerPlasmader Sonne, wo die Schichten nicht starr sind. Seine äquatoriale Rotationsgeschwindigkeit erreicht ungefähr2 km/s.

Physikalisches Interesse der Beziehung \(v = \frac{2\pi r}{T}\)

Das Wissen um dieRotationsgeschwindigkeiteines Sterns ist wichtig, um ihn zu verstehenphysikalische Eigenschaftenund seindynamische Prozesse. Es ist direkt mit dem verknüpftLänge des Sterntagesund gibt Hinweise dazuinnere EntwicklungUnddie Geschichte des Planeten.

Zum Beispiel amJupiter, die extrem schnelle Rotation (weniger als 10 Stunden) erzeugt immenseKonvektionszellenUndZyklonstürmeRiesen, der berühmteste davon ist derGroßer roter Fleck.

Der Zusammenhang zwischen Gravitation und Rotation

Die Planetenrotation resultiert aus einem Gleichgewicht zwischenAnziehungskraftund dieZentrifugalkraft. Dynamisches Gleichgewicht wird erreicht, wenn die Zentrifugalkraft an der Oberfläche wirktteilweise kompensiertSchwerkraft: \((\frac{G M m}{R^2} - m \omega^2 R \ approx 0)\) wobei \(G\) das istGravitationskonstante, \(M\) die Masse des Planeten, \(m\) die Masse eines Körpers auf der Oberfläche und \(R\) der Planetenradius. Diese Beziehung zeigt, dass die schnelle Rotation eines Planeten dazu neigt, die zu verringernscheinbare Schwerkraftam Äquator.

Dynamische Konsequenzen und Stabilität

Planeten behalten ihre Rotationsgeschwindigkeit nicht für immer bei. Unter der Wirkung vonGezeitenkräfte, ihr Drehimpuls kann auf ihren Satelliten oder auf ihre Umlaufbahn übertragen werden. Somit ist dieErdeallmählich verlangsamt, und dieMondbewegt sich pro Jahr um ca. 3,8 cm weg. Diese Energiedissipation tendiert zu einem Zustand vonsynchrone Rotation, wie es zwischen Mond und Erde beobachtet wird.

Die Rotationsstabilität hängt auch von der inneren Massenverteilung ab. Flüssige Planeten wieJupiterOderSaturnweisen aufgrund ihrer hohen Winkelgeschwindigkeit \((\omega)\ eine starke Abflachung auf), während Gesteinsplaneten, die steifer sind, dieser Verformung widerstandsfähiger gegenüberstehen.

Ursprung des Planetendrehimpulses

Während der Bildung vonprotoplanetare Scheibe, Kollisionen und lokale Einstürze führten zu einer bevorzugten Rotationsbewegung. Der Gesamtdrehimpuls verteilt sich auf die Sonne, die Planeten und ihre Satelliten. Diese Verteilung wurde bereits analysiert vonIsaac Newton(1643-1727) und später formalisiert vonLaplace(1749-1827) erklärt die nahezu gleichmäßige Rotation von Planetenkörpern um dieselbe Ekliptikebene.

Grundlegende Rotationsgleichungen

Wir definieren dielineare Geschwindigkeitvon einem Punkt auf der Oberfläche aus durch: \((v = \omega R)\) und dieRotationsperiode\(T\) durch: \((\omega = \frac{2\pi}{T})\)
Diese Gleichungen setzen die beobachtbaren Größen in Beziehung und ermöglichen die Berechnung der Länge des Planetentages. Zum Beispiel,Jupiter, mit einem Radius \(R = 71\.492 \text{ km}\) und \(T = 9,93 \text{ h}\), hat eine äquatoriale Geschwindigkeit \(v ≈ 12,6 \text{ km/s}\), viel höher als die der Erde \((0,465 \text{ km/s})\).

Hinweis: :
Die Kreiseleffekte eines rotierenden Planeten erklären diesPräzession der Tagundnachtgleicheund langsame Schwankungen der Achsenneigung. Diese Phänomene beeinflussen das Klima direkt auf Zeitskalen von mehreren tausend Jahren (Milankovitch-Zyklen).

Quelle :NASA Planetary Fact Sheet, Astronoo.