Letzte Aktualisierung: 9. April 2023

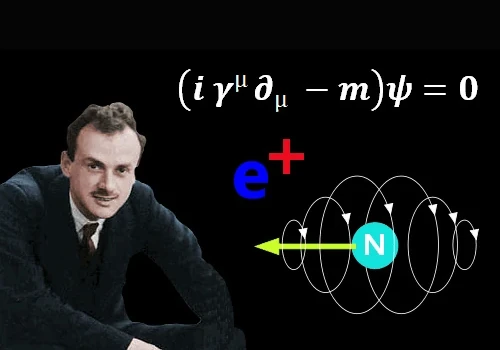
Dirac-Gleichung (1928)

(iγ^μ∂_μ-mc)ψ=0

L'Dirac-Gleichungwurde 1928 vom britischen theoretischen Physiker Paul Dirac (1902-1984) formuliert.
Die Dirac-Gleichung ist in der Quantenphysik wichtig, weil sie das Verhalten hochenergetischer Teilchen beschreiben kann, die sich mit Geschwindigkeiten nahe der Lichtgeschwindigkeit bewegen, wie etwa Elektronen, was mit den Gleichungen der klassischen Physik nicht genau beschrieben werden kann. In dieser Gleichung kombiniert Dirac die Quantenmechanik und die spezielle Relativitätstheorie von Albert Einstein.
Die Dirac-Gleichung hatte erhebliche Auswirkungen auf die Quantenphysik und führte zu vielen wichtigen Entdeckungen, beispielsweise zur Vorhersage der Existenz von Antimaterie.
Sie ist allgemeiner als die Schrödinger-Gleichung, die nur für nichtrelativistische Teilchen gilt.
Sie führte auch den Begriff des Spins (Eigendrehimpuls) von Teilchen ein, der eine grundlegende Eigenschaft subatomarer Teilchen ist.
Es ermöglichte auch, Phänomene wie die Vakuumpolarisation zu verstehen, bei der es sich um die spontane Bildung von Teilchen-Antiteilchen-Paaren aus dem Quantenvakuum handelt.

Die Dirac-Gleichung lautet: (iγ^μ∂_μ-mc)ψ=0
• Ich bin derimaginäre komplexe Zahl.
• γ^μ stellt eine Gammamatrix dar, die von einem Index μ abhängt. Gamma-Matrizen sind Matrizen der Dimension 4x4 (vier Dimensionen der Raum-Zeit), die zur Darstellung der Eigenschaften von verwendet werdendrehenTeilchen in der Dirac-Gleichung.
• ∂_μ ist der partielle Ableitungsoperator bezüglich der Raum-Zeit-Koordinate μ (∂/∂xμ) = (∂/∂t, ∂/∂x, ∂/∂y, ∂/∂z). Dieser partielle Ableitungsoperator ermöglicht es, unter Berücksichtigung relativistischer Effekte zu beschreiben, wie sich ein physikalisches Feld, beispielsweise das elektromagnetische Feld oder das Gravitationsfeld, in der Raumzeit ändert.
• m ist die Masse des Teilchens.
• es ist die Lichtgeschwindigkeit im Vakuum.
• ψ ist die Wellenfunktion, die den Quantenzustand des Teilchens beschreibt.

Wofür wird die Dirac-Gleichung verwendet?
• Die Dirac-Gleichung wird in der Quantenfeldtheorie zur Beschreibung von Wechselwirkungen zwischen Elementarteilchen verwendet und ist damit ein wesentliches mathematisches Werkzeug für die Teilchenphysik.
• Die Entdeckung der Existenz von Antiteilchen, insbesondere des Positrons (Antiteilchen des Elektrons), ermöglicht dessen Verwendung in der medizinischen Bildgebung.
Tatsächlich besteht die Positronenemissionstomographie darin, dem Patienten ein Radiotracer-Medikament zu injizieren, dessen radioaktives Isotop ein Emitter von β+-Strahlung, also ein Positronenemitter, ist. Diese Positronen vernichten sich bei Kontakt mit den Elektronen des umliegenden Gewebes sofort und es entstehen zwei Gammaphotonen. Die Detektion dieser Photonen ermöglicht es, den Ort ihrer Emission und die Konzentration des Tracers an jedem Punkt der Organe zu lokalisieren.
• Es ermöglicht die Erklärung der Feinstruktur der Spektrallinien von Wasserstoff. Diese Lichtlinien, die im Emissions- oder Absorptionsspektrum eines chemischen Elements erscheinen, werden durch den Übergang von Elektronen zwischen verschiedenen Energieniveaus in Atomen verursacht.
• Es ist nützlich in Elektron-Positron-Kollidern, die gleichzeitig zwei Teilchenstrahlen in entgegengesetzte Richtungen beschleunigen, einen aus Elektronen und einen aus Positronen. Bei diesen hochenergetischen Frontalkollisionen vernichten sich Elektronen und Positronen gegenseitig und setzen dabei beträchtliche Energie frei, die zur Bildung neuer Teilchen führt.

Die Dirac-Gleichung inspirierte andere Gleichungen, beispielsweise die Klein-Gordon-Gleichung, die spinlose Teilchen (Bosonen) wie Photonen beschreibt. Zusammenfassend lässt sich sagen, dass es sich um eine der wichtigsten Entwicklungen in der theoretischen Physik des 20. Jahrhunderts handelte und unser Verständnis des Universums erweiterte. Es ist möglich, dass die ersten Menschen, die den Mars erreichen, dies an Bord einer Positronen-Raumsonde tun.

L’unité imaginaire est représentée par la lettre i en mathématiques. Elle est définie comme la racine carrée de -1, c’est-à-dire que i² = -1.
L’unité imaginaire est utilisée pour représenter les nombres complexes, qui sont des nombres de la forme a + bi, où a et b sont des nombres réels. Les nombres complexes ont une partie réelle (a) et une partie imaginaire (b).
L’unité imaginaire est très utile en mathématiques, en physique et dans d’autres domaines scientifiques pour représenter des phénomènes qui ont une composante complexe. Par exemple, elle est utilisée dans l’analyse de circuits électriques en électronique, dans la résolution d’équations différentielles, et dans la représentation des ondes électromagnétiques en physique.
Il convient de noter que l’utilisation de l’unité imaginaire peut sembler abstraite ou étrange au début, mais elle permet d’étendre le domaine des nombres réels et offre une grande puissance de calcul pour la résolution de problèmes complexes. Le spin est une grandeur quantique qui caractérise la quantité de moment angulaire intrinsèque que possède une particule, indépendamment de son mouvement de translation ou de rotation dans l’espace. Il est mesuré en unités de la constante de Planck divisée par 2π, généralement exprimée en h/2π ou ħ (prononcé « h-barre »).
Le spin est un nombre quantique qui peut prendre des valeurs entières ou demi-entières, telles que 0, 1/2, 1, 3/2, etc.