Letzte Aktualisierung: 7. April 2023

Maxwells Gleichungen

Bildbeschreibung: Nach den Gleichungen von James Clerk Maxwell (1831-1879) ist Licht eine sich selbst ausbreitende elektromagnetische Transversalwelle mit elektrischen und magnetischen Komponenten, wobei die elektrischen und magnetischen Felder im rechten Winkel zueinander schwingen und sich senkrecht zu der Richtung, in der sie sich ausbreiten, unbegrenzt ausbreiten, sofern sie nicht von der dazwischen liegenden Materie absorbiert werden. Das heißt, jede Feldart – elektrische und magnetische – erzeugt die andere, um die gesamte Verbundstruktur mit endlicher Lichtgeschwindigkeit durch den leeren Raum auszubreiten.

Die 4 Gleichungen von Maxwell

Maxwell veröffentlichte seine Theorie erstmals 1865 in Form von zwanzig Gleichungen mit zwanzig Unbekannten, 1873 schrieb er seine Theorie dann in Form von acht Gleichungen um. Erst 1884 formulierte Oliver Heaviside (1850-1925) diese Gleichungen in Form der vier Vektor- und Skalargleichungen um.

Maxwells Gleichungen sind daher ein Satz von vier mathematischen Gleichungen, die die grundlegenden Eigenschaften elektromagnetischer Felder beschreiben, die für das Verständnis von Elektrizität und Magnetismus unerlässlich sind.
Das elektrische FeldE⃗wird durch mit ρ bezeichnete Teilchen erzeugt.
Das MagnetfeldB⃗entsteht durch Ströme, also bewegte Ladungen, bezeichnet mit J. Wenn ein Strom durch einen Kupferdraht fließt, entsteht ein Magnetfeld (dieser Strom führt dazu, dass die Nadel eines nahegelegenen Kompasses abweicht).
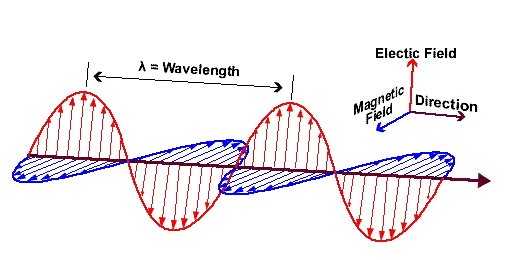
Viele Phänomene sind sowohl elektrischer als auch magnetischer Natur (Wellen einschließlich Licht, Elektrostatik, Batterien, elektromagnetische Induktion, Elektromagnete usw.).

Maxwells Gleichungen werden oft in Vektorschreibweise geschrieben, um elektromagnetische Felder darzustellen (E⃗UndB⃗).

• Maxwells erste Gleichung, auch Gaußsches Gesetz genannt, beschreibt, wie elektrischer Fluss durch eine geschlossene Oberfläche fließt.
∇.E = ρ/ε0
∇.E ist die Divergenz des elektrischen Feldes, die die Menge des elektrischen Flusses misst, der eine bestimmte Oberfläche verlässt.
ρ ist die elektrische Ladungsdichte im betrachteten Bereich und ε0 ist die Vakuumpermittivität, eine physikalische Konstante.

• Maxwells zweite Gleichung, auch Gaußsches Gesetz für Magnetismus genannt, besagt, dass der gesamte magnetische Fluss durch eine geschlossene Gaußsche Oberfläche immer Null ist.
∇.B = 0
∇.B ist die Magnetfelddivergenz, die die Menge des magnetischen Flusses misst, der eine bestimmte Oberfläche verlässt.

• Maxwells dritte Gleichung, auch Faradaysches Gesetz genannt, beschreibt, wie ein sich bewegendes Magnetfeld ein elektrisches Feld erzeugen kann.
∇ x E = -dB/dt
∇ x E ist die Rotation des elektrischen Feldes, die die Zirkulation des elektrischen Feldes um eine gegebene Schleife misst.
dB/dt ist die zeitliche Variation des Magnetfeldes.

• Maxwells vierte Gleichung, auch Ampère-Maxwell-Gesetz genannt, beschreibt, wie ein sich bewegendes elektrisches Feld ein magnetisches Feld erzeugen kann.
∇ x B = μ0(J + ε0*dE/dt)
∇ x B ist das rotierende Magnetfeld, das die Zirkulation des Magnetfelds um eine gegebene Schleife misst.
μ0 ist die Vakuumpermeabilität, eine weitere physikalische Konstante.
J ist die elektrische Stromdichte in der betrachteten Region und dE/dt ist die zeitliche Variation des elektrischen Feldes.

Maxwells Gesetze beschreiben das Verhalten elektrischer und magnetischer Felder und die Beziehung zwischen beiden. Somit beschreiben Maxwells Gleichungen, wie elektrische und magnetische Felder sich gegenseitig in Bewegung erzeugen können.