Alle elektromagnetischen Phänomene lassen sich auf ein System von vier grundlegenden Beziehungen reduzieren: die Maxwell-Gleichungen. Diese Gleichungen allein sagen alles über die Dynamik elektrischer und magnetischer Felder voraus.
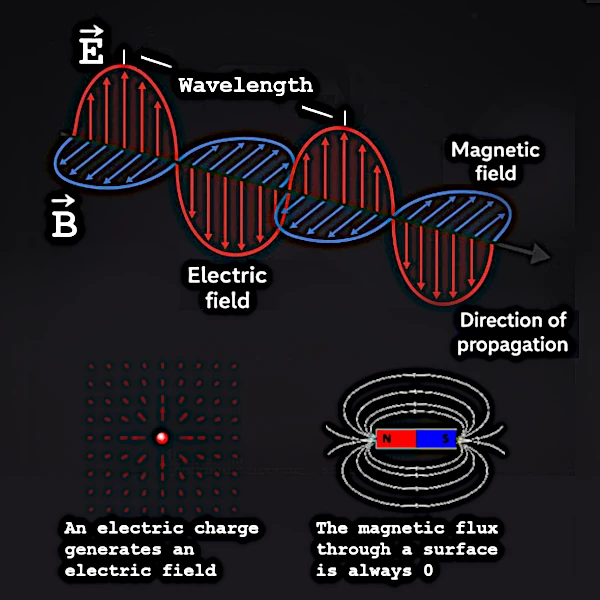
Die letzten beiden Gleichungen sind der Schlüssel zum Rätsel des Durchgehens. Ein sich zeitlich änderndes Magnetfeld (\( \partial \mathbf{B}/\partial t \)) erzeugt ein rotierendes elektrisches Feld. Symmetrisch dazu erzeugt ein sich änderndes elektrisches Feld (\( \partial \mathbf{E}/\partial t \)) ein rotierendes Magnetfeld. Es ist diese dynamische Kopplung, die sich während der Ausbreitung selbst erhält.
Als James Clerk Maxwell (1831–1879) im 19. Jahrhundert die Gesetze der Elektrizität und des Magnetismus vereinheitlichte, entdeckte er ein überraschendes Phänomen: Eine lokale Störung eines elektrischen oder magnetischen Feldes erzeugt eine Welle, die sich von selbst im Vakuum ausbreitet, ohne zusätzliche Energie zu benötigen.
Maxwell zeigte, dass sich diese Welle mit einer endlichen Geschwindigkeit ausbreitet, die durch zwei Eigenschaften des Vakuums bestimmt wird:
Die Formel \( c = \frac{1}{\sqrt{\mu_0 \varepsilon_0}} \) gibt diese Geschwindigkeit an.
Durch die Kombination der Gesetze von Faraday und Ampère-Maxwell erhielt er eine Wellengleichung. Durch Einsetzen der Werte von μ₀ und ε₀ fand er: \( c \approx 300.000 \) km/s, die Lichtgeschwindigkeit!
1865 schloss Maxwell, dass Licht eine elektromagnetische Welle ist, genau wie Radiowellen oder Mikrowellen. Eine Entdeckung, die die Physik revolutionierte.
N.B.:
Zu Maxwells Zeit (1865) war die Lichtgeschwindigkeit noch nicht mit großer Genauigkeit bekannt. Die verfügbaren experimentellen Messungen, die insbesondere von Armand Fizeau (1819-1896) und Albert Michelson (1852-1931) durchgeführt wurden, erlaubten es, \( v \) mit einem erheblichen Fehlerbereich zu schätzen. Maxwells theoretische Berechnung ergab daher einen Wert, der dem, was später bestätigt wurde, sehr nahe kam, was eine beeindruckende Bestätigung seiner Theorie darstellte.
Als Maxwell die Gesetze der Elektrizität und des Magnetismus zusammenfügte, entdeckte er eine sich selbst erhaltende Struktur, sobald ein elektrisches oder magnetisches Feld lokal gestört wird. Dieses "Durchgehen" ist stabil, ohne Verstärkung, und besitzt keine interne Energiequelle. Das Vakuum trägt die Welle, ohne sie zu speisen.
Diese dynamische Schleife zwischen \( \mathbf{B} \) und \( \mathbf{E} \) erzeugt eine Struktur, die sich im Vakuum mit endlicher Geschwindigkeit ausbreitet.
Der Term \(\mu_0 \varepsilon_0\) der vierten Gleichung legt die Lichtgeschwindigkeit fest: \( c = \frac{1}{\sqrt{\mu_0 \varepsilon_0}}. \)
Durch mathematische Kombination der Gesetze von Faraday und Ampère-Maxwell (durch Bildung der Rotation des einen und Verwendung des anderen) wird die Kopplung eliminiert, um eine Gleichung zu erhalten, die jedes Feld einzeln beschreibt.
Für das elektrische Feld findet man: \( \nabla^2 \mathbf{E} = \mu_0 \varepsilon_0 \frac{\partial^2 \mathbf{E}}{\partial t^2} \) Dies ist die klassische Form der Wellengleichung. Der Term \( \mu_0 \varepsilon_0 \) steht vor der zweiten Zeitableitung. In der mathematischen Physik wird die Standard-Wellengleichung als \( \nabla^2 \psi = \frac{1}{v^2} \frac{\partial^2 \psi}{\partial t^2} \) geschrieben, wobei \( v \) die Ausbreitungsgeschwindigkeit ist.
Durch direkte Identifikation: \( \frac{1}{v^2} = \mu_0 \varepsilon_0 \quad \Rightarrow \quad v = \frac{1}{\sqrt{\mu_0 \varepsilon_0}} \)
Maxwell berechnete diesen Wert mit den Konstanten, die zu seiner Zeit bekannt waren:
Das Ergebnis ist erstaunlich: \( v \approx 2.998 \times 10^{8} \, \text{m/s} \), die Geschwindigkeit der Wellen entspricht der experimentell gemessenen Lichtgeschwindigkeit!
N.B.:
Diese mathematische Demonstration setzt ein Vakuum voraus, d.h. das Fehlen von Ladungen und Strömen (\( \rho = 0, \, \mathbf{J} = 0 \)). Die Argumentation besteht darin, die Rotation des Faradayschen Gesetzes zu nehmen und die vektorielle Identität \( \nabla \times (\nabla \times \mathbf{E}) = \nabla(\nabla \cdot \mathbf{E}) - \nabla^2 \mathbf{E} \) zu verwenden, kombiniert mit dem Gaußschen Gesetz (\( \nabla \cdot \mathbf{E} = 0 \) im Vakuum) und dem Ampère-Maxwell-Gesetz. Man erhält so dieselbe Wellengleichung für das Magnetfeld \( \mathbf{B} \). Diese theoretische Vorhersage von James Clerk Maxwell (1831-1879) aus dem Jahr 1865 wurde 1887 von Heinrich Hertz (1857-1894) experimentell bestätigt, als er die ersten Funkwellen erzeugte.
Maxwell fand heraus, dass sich elektromagnetische Wellen mit einer bestimmten Geschwindigkeit im Vakuum ausbreiten, aber der Nachweis, dass dies eine Grenzgeschwindigkeit ist, war noch nicht erbracht. Maxwell kannte die Relativitätstheorie noch nicht. Er hatte daher keinen Grund zu glauben, dass es sich um eine universelle Grenzgeschwindigkeit handelte. Die Vorstellung einer universellen Grenze entstand erst mit der speziellen Relativitätstheorie, lange nach Maxwell.
Erst mit der speziellen Relativitätstheorie (1905) von Albert Einstein (1879-1955) wurde die Lichtgeschwindigkeit im Vakuum \( c \) als die maximale Geschwindigkeit, mit der sich Information, Energie oder jede physikalische Wechselwirkung ausbreiten kann, anerkannt. Mit anderen Worten, \( c \) ist eine grundlegende Grenze, die durch die Struktur von Raum und Zeit auferlegt wird, und nicht nur eine Folge der Maxwell-Gleichungen.
Elektromagnetische Phänomene gehorchen den Maxwell-Gleichungen und lassen sich wie folgt zusammenfassen:
Somit sind Licht und alle elektromagnetischen Wellen nichts anderes als die Manifestation dieses Phänomens der Selbsterhaltung der elektrischen und magnetischen Felder im Vakuum.
Das Elektromagnetische Durchgehen: Das Geheimnis der Lichtgeschwindigkeit 
Das photoelektrische Effekt verstehen: Licht und Elektronen 
Wie weit ist der Horizont entfernt? 
Wie speisen Solarmodule Strom ins Netz ein? 
Impulsdynamik zur Erklärung des Antriebs von Raketen oder Quallen 
Energieverteilung der Elektronen in Atomen 
Heisenbergs Unschärferelation: Quantenunsicherheit verstehen 
Zusammenhang zwischen Energie, Leistung und Zeit 
Warum gibt es eine Grenze für Kälte, aber nicht für Wärme? 
Galileis Fallgesetz 
Das Gesetz der idealen Gase 
Schrödingergleichung und Atomstruktur 
Noethers Theorem: Energieerhaltung aus Symmetrien 
Verhältnis zwischen schwerer und träger Masse und das Äquivalenzprinzip 
Die dritte grundlegende Gleichung der Physik 
Die zweite grundlegende Gleichung der Physik 
Die erste grundlegende Gleichung der Physik 
Die elektromagnetische Kraft oder Lorentzkraft 
Die empfangene Sonnenenergie variiert mit der Neigung 
Warum ist Marmor kälter als Holz? 
Warum hat ein Photon ohne Masse Energie? 
Bayes-Formel und künstliche Intelligenz 
Die sieben fundamentalen Konstanten der Physik 
Welche Temperatur herrscht im interstellaren Raum? 
Strahlungskurven des schwarzen Körpers: Plancks Gesetz 
Das Äquivalenzprinzip: Gravitationseffekte sind von Beschleunigungen nicht unterscheidbar 
E=mc²: Die vier fundamentalen Konzepte des Universums überdacht 
Wie wiegt man die Sonne? 
Gleichung des freien Falls (1604) 
Coulomb-Gleichung (1785) 
Boltzmann-Gleichung zur Entropie (1877) 
Gleichungen der speziellen Relativität (1905) 
Gleichung der allgemeinen Relativität (1915) 
Gleichungen der Planetenrotation: Zwischen Drehimpuls und gravitativer Balance 
Gleichung der Orbitgeschwindigkeit eines Planeten 
Plancks Gleichung 
Schrödingergleichung 
Wie beschreiben Newtons drei Gesetze die gesamte klassische Mechanik? 
Maxwells Gleichungen 
Dirac-Gleichung 
Energieerhaltung 
Gleichung der elektromagnetischen Induktion 
Warum haben Elementarteilchen keine Masse? 
Unterschied zwischen Wärme und Temperatur