Die Schrödinger-Gleichung revolutionierte unsere Sicht auf die Materie

Von der Gewissheit zur Wahrscheinlichkeit: Das Atom nach Schrödinger

Stellen Sie sich vor, dass im Atom das Elektron nicht mehr wie ein kleiner Planet ist, der ordentlich um einen sonnenähnlichen Kern kreist, sondern eine Musiknote, eine Schwingung, eine Welle. Dies ist die konzeptionelle Revolution, die von Erwin Schrödinger (1887-1961) im Jahr 1926 ausgelöst wurde.

Die Schrödinger-Gleichung (grundgleichung der Quantenmechanik, die die Entwicklung eines Teilchens durch eine Wellenfunktion beschreibt.) sagt uns nicht, wo sich das Elektron mit Sicherheit befindet, sondern wo es sich wahrscheinlich aufhält. Sie verwandelt den möglichen atomaren Raum in eine Tanzfläche, auf der die Figuren des Tänzers die wahrscheinlichen Orbitale zeichnen.

Die Schrödinger-Gleichung verstehen, ohne sich zu komplizieren

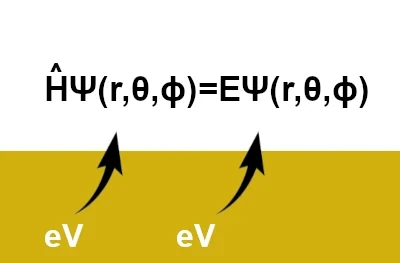
Die Schrödinger-Gleichung lautet: \(\hat{H}\,\Psi(r,\theta,\phi)=E\,\Psi(r,\theta,\phi)\), wobei \((r, \theta, \phi)\) Kugelkoordinaten sind (r: radiale Koordinate, θ: Polarwinkel, ϕ: Azimutwinkel). In ihrer einfachsten Form wird sie jedoch geschrieben als: \( \hat{H} \Psi = E \Psi \)

Um die Geheimnisse des Atoms zu entschlüsseln, wird ein besonderer Schlüssel benötigt. Dieser Schlüssel ist das, was Physiker die "Wellenfunktion" nennen. Sie hat einen eleganten Namen: Ψ (ausgesprochen "Psi", wie der Anfang von "Psyche" oder Neptuns Dreizack).

Wie liest man einfach \( \hat{H} \Psi = E \Psi \)?

Stellen Sie sich vor, Ψ ist eine Art "Navigationskarte" für das Elektron. Diese Karte sagt nicht, wohin das Elektron gehen wird, sondern wohin es gehen kann. Genauer gesagt, beschreibt sie die Orte, an denen Sie es wahrscheinlich finden werden, und die Orte, an denen Sie es nicht finden werden.

Links steht \(\hat{H}\) für "alles, was im Atom passiert" (die Anziehung des Kerns, die Energie, die Einschränkungen). Rechts steht \(E\) für das Ergebnis: die Energie, die das Elektron haben muss, um in dieser Konfiguration stabil zu sein.

Diese Gleichung zu lösen, ist wie die richtige Note auf einem Klavier zu finden, damit sie in einem Raum perfekt widerhallt. Man kann nicht einfach irgendetwas spielen: Nur bestimmte Noten (Energien \(E\)) und bestimmte Schwingungsarten (Funktionen Ψ) funktionieren harmonisch.

Aber wie sieht Ψ aus?

Dies war das große Dilemma der Physiker, bis Max Born (1882-1970) eine geniale Intuition hatte. Er sagte: "Schauen Sie nicht auf Ψ selbst, sondern auf ihr Spiegelbild, ihr Quadrat, \(|\Psi|^2\)". Es ist wie der Rauch, der eine Wahrscheinlichkeitswolke offenbart, wo sich das Objekt befand, bevor der Magier es verschwinden ließ. So gibt \(|\Psi|^2\) Punkt für Punkt im Raum um den Kern die Wahrscheinlichkeit für die Anwesenheit des Elektrons an.

Kurz gesagt, wo \(|\Psi|^2\) groß ist, ist der "Garten" des Atoms, wo das Elektron seine Zeit verbringt. Wo \(|\Psi|^2\) null ist, ist eine "Wüste", das Elektron kommt nie dorthin. Das Elektron wird dann weniger zu einer Kugel und mehr zu einer Wolke, einer Lichtspur, einem eleganten und verschwommenen Tanz um den Kern, genannt "Orbital".

Die Muster des Elektronentanzes: Die Atomorbitale

Angewendet auf das Wasserstoffatom (ein Proton und ein Elektron) offenbart die Schrödinger-Gleichung eine Reihe von Lösungen, Quantenzuständen, die jeweils durch drei Zahlen, oft Quantenzahlen genannt, charakterisiert sind. Jede Lösung entspricht einem Atomorbital, einer spezifischen dreidimensionalen geometrischen Form, die die bevorzugte "Tanzzone" des Elektrons ist.

Wo Niels Bohr (1885-1962) Elektronen sah, die auf ordentlichen kreisförmigen Bahnen wie Planeten um die Sonne umlaufen, zeigt die Schrödinger-Gleichung ein viel reicheres und poetischeres Universum. Die Lösungen zeichnen im Raum geometrische Formen von eleganter Komplexität.

• Die perfekte Kugel (s-Orbital): Das einfachste davon, 1s genannt, ist eine Kugel. Das Elektron hat keine bevorzugte Richtung; es ist homogen um den Kern herum vorhanden, wie ein perfekt symmetrischer Nebel.
• Die Hanteln (p-Orbitale): Sobald man sich ein wenig vom Kern entfernt (zweites Energieniveau), strukturiert sich der Raum. Dann erscheinen drei identische "Hantel"-Formen, die jeweils in eine Raumrichtung (entlang der x-, y- und z-Achsen) zeigen. Das Elektron konzentriert sich dann in zwei gegenüberliegenden Lappen, auf beiden Seiten einer Stillezone (der Knotenebene).
• Die Blumen der Materie (d- und f-Orbitale): In noch größeren Entfernungen bereichert sich die Choreografie. Die d-Orbitale nehmen Geometrien an, die an vierblättrige Kleeblätter erinnern. Die f-Orbitale entfalten multiple Blütenblätter in noch ausgefeilteren Anordnungen. Echte mathematische Signaturen des Raumes, sie sind für die Chemie das, was Tonleitern für die Musik sind: die grundlegende Struktur, die alle Kombinationen, alle Moleküle, die gesamte uns umgebende Materie ermöglicht.

Diese Formen sind keine bloßen mathematischen Fantasien. Sie sind der Eckstein der Chemie. Die Geometrie der Orbitale bestimmt, wie Atome sich verbinden können, um Moleküle zu bilden. Die Richtung der p-Orbitale erklärt zum Beispiel die gewinkelte Form des Wassermoleküls (H₂O). Der Reichtum der d-Orbitale ist verantwortlich für die leuchtenden Farben der Ionen der Übergangsmetalle. So ist die Schrödinger-Gleichung durch ihre Lösungen die verborgene Grammatik, die die Struktur aller Materie um uns herum diktiert.

N.B.:
Das mentale Bild der "Elektronenwolke" ist genauer als das der "bewegten Teilchen". Ein Orbital ist eine Momentaufnahme der Wahrscheinlichkeitsverteilung. Wenn Sie ein ultra-schnelles Foto des Atoms machen würden, würden Sie das Elektron an einem Punkt sehen; durch das Überlagern von Millionen solcher Fotos würde die Form des Orbitals erscheinen, wie eine Lichtspur, die ein Tänzer auf einer dunklen Bühne hinterlässt.