シュレーディンガー方程式は物質の見方を革命的に変えました

確実性から確率へ：シュレーディンガーによる原子

原子の中で電子が太陽のような核の周りを規則正しく回る小さな惑星ではなく、音楽の音符、振動、波であると想像してみてください。 これが、エルヴィン・シュレーディンガー（1887-1961年）が1926年に引き起こした概念的革命です。

シュレーディンガー方程式 (量子力学の基本方程式で、波動関数によって粒子の進化を記述します。)は、電子がどこにあるかを確実に教えてくれるのではなく、どこに存在する可能性があるかを示します。 この方程式は、可能な原子空間をダンスフロアに変え、ダンサーの動きが確率的な軌道を描きます。

複雑にならずにシュレーディンガー方程式を理解する

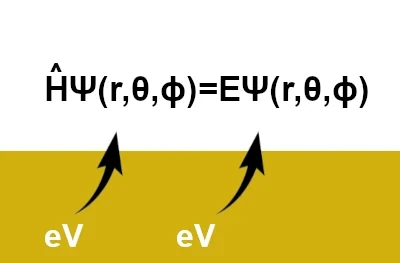
シュレーディンガー方程式は次のように書かれます：\(\hat{H}\,\Psi(r,\theta,\phi)=E\,\Psi(r,\theta,\phi)\)。ここで、\((r, \theta, \phi)\)は球座標（r：動径座標、θ：極座標、ϕ：方位角座標）です。 しかし、最も簡単な形式では次のように書かれます：\( \hat{H} \Psi = E \Psi \)

原子の謎を解くには特別な鍵が必要です。 この鍵は物理学者が「波動関数」と呼ぶものです。 この関数には、Ψ（「プサイ」と読み、「サイキ」の始まりやネプチューンの三叉槍のように）という洗練された名前が付けられています。

\( \hat{H} \Psi = E \Psi \)を簡単に読むには？

Ψを電子のための「ナビゲーションマップ」のようなものと想像してください。 このマップは電子がどこに行くかではなく、どこに行けるかを示します。 より正確には、電子を見つける可能性のある場所と、見つからない場所を記述します。

左側の\(\hat{H}\)は「原子内で起こるすべてのこと」（核の引力、エネルギー、制約）を表します。 右側の\(E\)は結果であり、電子がこの構成で安定するために持つべきエネルギーです。

この方程式を解くことは、部屋で完璧に響くピアノの正しい音を見つけるようなものです。 何でも弾けるわけではありません：特定の音（エネルギー\(E\)）と特定の振動の仕方（関数Ψ）だけが調和して機能します。

しかし、Ψはどのようなものですか？

これは、マックス・ボルン（1882-1970年）が天才的な直感を持つまで、物理学者たちの大きなジレンマでした。 彼は、「Ψそのものを見るのではなく、その反射、つまり二乗\(|\Psi|^2\)を見なさい」と言いました。 これは、魔術師が物体を消す前にあった確率の雲を明らかにする煙のようなものです。 このように、\(|\Psi|^2\)は、核の周りの空間の各点で電子が存在する確率を示します。

つまり、\(|\Psi|^2\)が大きいところは原子の「庭」であり、電子が時間を過ごす場所です。 \(|\Psi|^2\)がゼロの場所は「砂漠」であり、電子は決して来ません。 電子はボールというよりも、雲、光の軌跡、核の周りの優雅でぼんやりとしたダンス、「軌道」となります。

電子のダンスのパターン：原子軌道

水素原子（1つの陽子と1つの電子）に適用すると、シュレーディンガー方程式は一連の解、量子状態を明らかにします。それぞれは3つの数、しばしば量子数と呼ばれるものによって特徴づけられます。 各解は原子軌道に対応し、電子の特権的な「ダンスゾーン」である特定の三次元幾何学的形状です。

ニールス・ボーア（1885-1962年）が、太陽の周りを回る惑星のように整然とした円軌道を回る電子を見た場所で、シュレーディンガー方程式ははるかに豊かで詩的な宇宙を明らかにします。 解は、優雅な複雑さを持つ幾何学的形状を空間に描きます。

• 完全な球（s軌道）: 最も単純なものは1sと呼ばれ、球です。電子は優先方向がなく、核の周りに均一に存在し、完全に対称な霧のように見えます。
• ダンベル（p軌道）: 核から少し離れると（第二エネルギーレベル）、空間が構造化されます。すると、3つの同じ「ダンベル」形状が現れ、それぞれが空間の方向（x、y、z軸に沿って）を指します。電子は、ノード面と呼ばれる静かな領域を挟んで、2つの反対側のローブに集中します。
• 物質の花（d軌道とf軌道）: さらに遠くでは、振付が豊かになります。d軌道は四つ葉のクローバーを思わせる幾何学的形状を持ちます。f軌道は、さらに複雑な配列の複数の花弁を展開します。これらは空間の数学的な署名であり、化学において音階が音楽にとってそうであるように、すべての組み合わせ、すべての分子、私たちを取り巻くすべての物質の基本構造です。

これらの形状は単なる数学的な空想ではありません。 これらは化学の要です。 軌道の幾何学は、原子が分子を形成するためにどのように結合できるかを決定します。 例えば、p軌道の方向は水分子（H₂O）の角度形状を説明します。 d軌道の豊かさは、遷移金属イオンの鮮やかな色の原因です。 このように、シュレーディンガー方程式はその解を通じて、私たちを取り巻くすべての物質の構造を決定する隠れた文法です。

N.B.：
「電子雲」のメンタルイメージは、「運動する粒子」のイメージよりも正確です。軌道は瞬間的な確率マップです。原子の超高速写真を撮ると、電子を1点で見ることができます。何百万枚ものこのような写真を重ね合わせると、軌道の形が現れます。暗いステージでダンサーが残した光の軌跡のようです。