最終更新日：2025年8月9日

電子のエネルギーが化学的性質を決定する仕組み

電子のエネルギーとは何ですか？

電子のエネルギーは、原子内の電子が持つ総エネルギーで、核からの距離とその運動によって決まります。このエネルギーは、特定の量子化された値のみを取ることができ、これをエネルギーレベルと呼びます。

原子物理学の基準となる水素原子を例に取りましょう。電子は基底状態（n=1で-13.6 eV）から励起状態（-3.4 eV、-1.51 eV、-0.85 eV...）へと移行し、最終的に0 eVで完全にイオン化します。これらのレベルはすべて、E_n = -13.6/n²の式で計算され、他の元素の結合エネルギーを比較するための基準としても使用されます。

電子エネルギーのこの量子化された性質が、化学元素の多様性とその挙動を説明します。その理解は、量子化学、材料科学、光合成、細胞呼吸、太陽電池など、多くの分野で不可欠です。

電子エネルギーと化学的性質の関係

多電子原子では、電子のエネルギーは核からの距離だけで決まるのではなく、核の引力と他の電子による反発との複雑な相互作用によって決まります。この微妙に調整された有効エネルギーが、原子が電子を失う、獲得する、または共有する傾向を決定し、その結果、その特徴的な化学的性質が現れます。つまり、電子エネルギーは元素の化学的なアイデンティティと、他の原子との相互作用の仕方を定義します。これが、ナトリウムが水と激しく反応するのに対し、ネオンが完全に不活性である理由を説明します。

炭素：具体例で理解する

電子エネルギーが化学的挙動をどのように決定するかを具体的に説明するために、生命の基本元素である炭素（Z = 6）を例に取りましょう。

その電子配置1s² 2s² 2p²は、6つの電子が3つの異なるエネルギーレベルを占めていることを示しています：1s殻の2つの電子は非常に強く結合しています（低エネルギー、-489.6 eV）、2s殻の電子は中間のエネルギーを持ち、2p殻の2つの価電子は弱く結合しています（高エネルギー、-30.6 eV）、そのため化学結合を形成するのに利用可能です。

高エネルギーと低エネルギー：混乱に注意

• 核から遠い（外殻） → 高エネルギー（0 eVに近い） → 取り除きやすい → 反応性が高い
• 核に近い（内殻） → 低エネルギー（非常に負） → 取り除きにくい → 不活性

「高エネルギー」の電子（例えば2p殻の-30.6 eVの電子）は核との結合が弱く、完全に取り除くのに30.6 eVだけ必要です。逆に、「低エネルギー」の電子（例えば1s殻の-489.6 eVの電子）は強く結合しており、解放するのに489.6 eVが必要です。

高所にある物体を想像してください：高いほど位置エネルギーが大きく、落ちやすくなります。「高エネルギー」軌道の電子はこの物体のようなもので、エネルギースケールの「高い」位置にあり（安定性が低い）、簡単に「落ち」（反応し）、より安定な状態に達します。

電子配置から分子構造へ

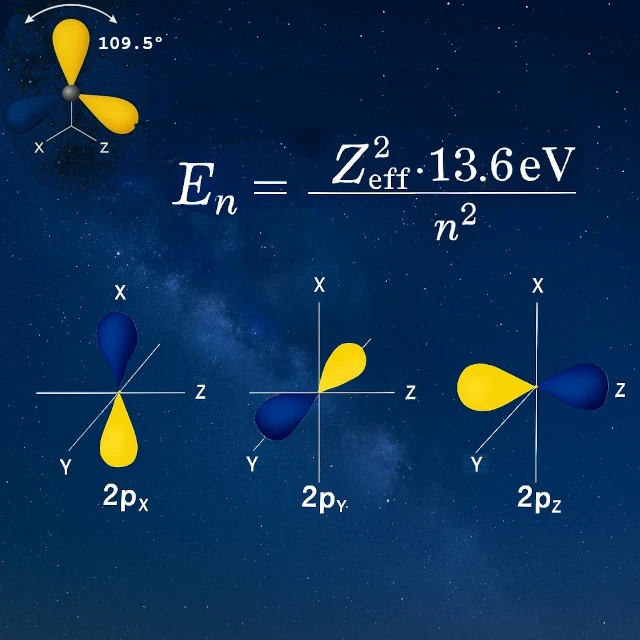
孤立した状態の炭素は、2p軌道（pₓとpᵧ）に2つの不対電子を持ち、これは2つの結合しか形成できないことを示唆します。しかし、炭素は4つの等価な結合を形成します。どうやって？ sp³混成と呼ばれる過程を経て：2s軌道が3つの2p軌道と融合し、4つの新しい等価な混成軌道を作り出します。

混成前（孤立した炭素）：

1s軌道：2電子（飽和）
2s軌道：2電子（飽和）
2p軌道：2電子が分布（pₓ ↑, pᵧ ↑, pz 空）

sp³混成後：

1s軌道：2電子（変化なし）
4つのsp³混成軌道（4つの「箱」が利用可能）、それぞれに1つの不対電子（109.5°の正四面体に向かって配向）

この正確な正四面体構造により、炭素は4つの強い結合を明確に定義された方向に形成することができます。均一な分布とは異なり、価電子は互いに109.5°の特権的な方向に局在化されています。この方向性のある四価性が、炭素を生命の分子的建築家とし、鎖、環、そして莫大な多様性を持つ三次元構造を構築することを可能にします。これはすべての有機化学の基礎です。