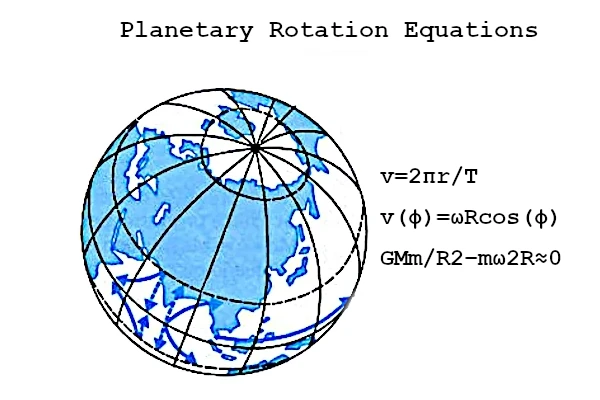
この方程式を説明するために、太陽系のいくつかの特徴的な例を挙げます。 半径が \(r = 6,371 \text{ km}\)、自転周期が \(T = 24 \text{ h}\) の地球の 赤道速度は約 \(v = \frac{2\pi r}{T} ≈ 1,670 \text{ km/h}\) です。
半径が \(r = 3,389 \text{ km}\)、自転周期が \(T = 24 \text{ h } 36 \text{ min}\) の火星は、 より遅く自転し、火星の赤道における速度は約 \(868 \text{ km/h}\) です。
この関係は、自転速度が惑星の半径と恒星日の長さに直接依存することを示しています。 大きな惑星や速く自転する惑星は、赤道での自転速度が高くなります。 逆に、コンパクトな惑星や遅い惑星は、線速度が低くなります。
最後に、この速度は赤道でのみ有効であることに注意することが重要です。 極に近づくにつれて、自転軸からの距離が減少し、自転速度は \(v(\phi) = \omega R \cos(\phi)\) になります。 ここで \(\phi\) は緯度です。したがって、自転周期は地球上のすべての点で同じ（地球の場合は24時間）ですが、 線速度は極に向かって連続的に減少し、極ではゼロになります。
惑星の自転運動は、その角運動量 \(L\) によって支配されます。これは基本的な関係式で定義されます： \((L = I \omega)\) ここで \(I\) は慣性モーメント、\(\omega\) は角速度です。 この方程式は、質量の軸周りの分布と回転の速さを表します。平衡状態にある惑星は、外部からの力がトルクを及ぼさない限り、その角運動量を保持します。
北極と南極では、自転速度は実際にはゼロです。これらの点は地球の自転軸と一致するためです。 したがって、地球が自転しても、極はこの軸に対して静止しています。極は円を描かず、低緯度の点とは異なります。
約6億年前、地球の1日は約22時間でした。 これは、地球が現在よりも速く自転していたことを示しています。 自転の徐々な減速は、月との重力相互作用によるもので、潮汐ブレーキとして知られています。
この単純な関係は普遍的ではありません。これは、固体の一様な自転、例えば地球型惑星にはよく適用されますが、 恒星の流体構造による差動回転には適用されません。 言い換えれば、自転周期は緯度に依存します：赤道地域は極地域よりも速く自転します。
太陽の場合、自転周期は赤道で約25日から極で約34日まで変化します。 この違いは、太陽のプラズマの性質を反映しており、層が剛体ではありません。 太陽の赤道における自転速度は約2 km/sです。
天体の自転速度を知ることは、その物理的特性と 動的プロセスを理解するために不可欠です。 これは恒星日の長さに直接関連し、内部進化と 惑星の歴史についての手がかりを提供します。
例えば、木星では、極めて速い自転（10時間未満）により、巨大な対流セルと 巨大なサイクロン嵐が生じます。その中で最も有名なのが大赤斑です。
惑星の自転は、重力と遠心力のバランスの結果です。 力学的平衡は、遠心力が表面で重力を部分的に相殺するときに達成されます： \((\frac{G M m}{R^2} - m \omega^2 R \approx 0)\) ここで \(G\) は重力定数、\(M\) は惑星の質量、\(m\) は表面の物体の質量、\(R\) は惑星の半径です。 この関係は、惑星の速い自転が赤道での見かけの重力を減少させる傾向があることを示しています。
惑星は永遠に自転速度を保持しません。潮汐力の影響下で、角運動量は衛星や軌道に移動する可能性があります。 したがって、地球は徐々に減速し、月は年間約3.8 cmずつ遠ざかっています。このエネルギーの散逸は、同期回転の状態、つまり月と地球の間で観察されるような状態に向かっています。
回転の安定性は、内部の質量分布にも依存します。木星や土星のような流体惑星は、高い角速度 \((\omega)\) により強い扁平化を示しますが、より剛体の岩石惑星はこの変形に対してより抵抗します。
原始惑星系円盤の形成時、衝突と局所的な崩壊により優先的な回転運動が課されました。 全体的な角運動量は、太陽、惑星、およびその衛星の間で分配されました。 この分配は、アイザック・ニュートン（1643-1727）によって既に分析され、後にラプラス（1749-1827）によって形式化され、惑星天体のほぼ一様な回転が同じ黄道面上で説明されます。
表面上の点の線速度は次のように定義されます： \((v = \omega R)\) 自転周期 \(T\) は次のように定義されます： \((\omega = \frac{2\pi}{T})\)
これらの方程式は観測可能な量を関連付け、惑星の1日の長さを計算することを可能にします。 例えば、半径 \(R = 71,492 \text{ km}\)、\(T = 9.93 \text{ h}\) の木星は、赤道速度 \(v ≈ 12.6 \text{ km/s}\) を持ち、これは地球の速度 \((0.465 \text{ km/s})\) よりもはるかに高いです。
N.B.：
回転する惑星のジャイロ効果は、分点の歳差運動と軸の傾斜のゆっくりとした変化を説明します。これらの現象は、数千年の時間スケール（ミランコビッチサイクル）で気候に直接影響を与えます。
| 惑星 | 自転周期（時間） | 自転周期（日） | 赤道速度（km/s） | 扁平率 | コメント |
|---|---|---|---|---|---|
| 水星 | 1407.6 | 58.65 | 0.003 | ≈ 0 | 遅い自転、太陽にほぼ固定 |
| 金星 | -5832.5 | -243.0 | 0.0018 | ≈ 0 | 非常に遅い逆行自転 |
| 地球 | 23.93 | 1.0 | 0.465 | 1/298 | 適度な自転、安定したバランス |
| 火星 | 24.62 | 1.03 | 0.241 | 1/169 | 地球よりやや遅い自転 |
| 木星 | 9.93 | 0.41 | 12.6 | 1/15 | 速い自転、強い扁平化 |
| 土星 | 10.7 | 0.45 | 9.9 | 1/10 | 速い自転、流体の内部構造 |
| 天王星 | -17.2 | -0.72 | 2.59 | 1/43 | 逆行自転、強く傾いた軸 |
| 海王星 | 16.11 | 0.67 | 2.68 | 1/58 | 速い自転、強い風と乱流 |
ソース：NASA Planetary Fact Sheet、 Astronoo。
光速：宇宙の絶対的な限界を超えられない理由 
現実は我々の手の届かないところに：証明できない真実 
50の方程式で解き明かす宇宙の物理：取扱説明書 
カヤ方程式：脱炭素化を複雑にする方程式 
宇宙における超えられない速度：エネルギーが無限になるとき 
電磁的暴走：光速の秘密 
光電効果を理解する：光と電子 
地平線はどれくらいの距離にあるのか？ 
太陽光パネルはどのように電気を電力網に送り込むのか？ 
運動量の力学：ロケットやクラゲの推進を説明する 
電子のエネルギーが化学的性質を決定する仕組み 
量子不確定性の重要な役割：どの粒子も静止することはできない 
エネルギーとパワー：混同しないで、時間がすべての違いを生む 
なぜ寒さには限界があるのに暑さにはないのか？ 
ガリレオの落体の法則 
理想気体の法則：一つの方程式、無数の応用 
シュレーディンガー方程式は物質の見方を革命的に変えました 
ネーターの定理の魔法：最小作用の原理から保存則へ 
重力質量と慣性質量の等価性と等価原理
物理学の第三方程式：衝突を理解するための運動量 
物理学の第二の基本方程式：保存される量の直感 
物理学の第一方程式：力を数学的に表現する方法 
電磁力またはローレンツ力 
受け取る太陽エネルギーは傾斜角によって変化する 
なぜ大理石は木よりも冷たいのか？ 
なぜ質量のない光子がエネルギーを持つのか？ 
ベイズの定理と人工知能 
物理学の7つの基本定数 
星間空間で感じる温度はどれくらいか？ 
黒体放射の曲線：プランクの法則 
等価原理：重力効果は加速度と区別がつかない 
E=mc²：宇宙の4つの基本概念を再考する 
太陽の重さを測る方法 
自由落下の方程式（1604年） 
クーロン vs ニュートン：宇宙の力の神秘的な類似性 
エントロピーに関するボルツマンの方程式（1877年） 
特殊相対性理論の方程式（1905年） 
一般相対性理論の方程式（1915年） 
惑星の自転方程式：角運動量と重力平衡の間 
惑星の公転速度の方程式 
プランクの方程式 
数学なしでシュレディンガー方程式を理解する 
ニュートンの三法則：落ちるリンゴから惑星の軌道まで 
マクスウェルの方程式 
ディラックの方程式 
エネルギー保存則 
電磁誘導の方程式 
なぜ素粒子は質量を持たないのか？ 
熱と温度の違い