最終更新日: 2025 年 8 月 29 日

多電子原子内の電子のエネルギー分布

画像の説明: 電子は量子数によって定義される特定の軌道を占めており、そのエネルギーは原子内の位置に依存します。画像出典:astronoo.com

電子エネルギーの紹介

L'電子エネルギーで多電子原子量子力学の中心的な概念です。電子を 1 つだけ持つ水素原子とは異なり、多電子原子には、相互作用および原子核と相互作用する複数の電子が含まれています。これらの複雑な相互作用により、電子エネルギーの計算はより困難になりますが、元素の化学的および物理的特性を理解するためには不可欠です。

電子のエネルギーによって、元素の原子構造や性質を理解することができます。シュレーディンガー方程式、原子軌道、スクリーニング効果は、エネルギー準位と電子配置を決定する上で重要な役割を果たします。

シュレディンガー方程式と原子軌道

原子内の電子のエネルギーは次のように記述されます。シュレーディンガー方程式、量子力学の基本方程式。多電子原子の場合、シュレーディンガー方程式は次のように記述されます。

\[ \hat{H} \Psi = E \Psi \]

ここで、 \(\hat{H}\) はハミルトニアン演算子、 \(\Psi\) は電子の波動関数、 \(E\) はこの状態に関連するエネルギーです。ハミルトニアンには運動エネルギーと位置エネルギーという用語が含まれており、後者では電子と原子核の間の相互作用、および電子自体の間の相互作用が考慮されます。

この方程式の解は次のようになります。原子軌道を説明します。原子核周囲の電子の空間分布。各軌道は、主量子数 \(n\)、方位角量子数 \(l\)、磁気量子数 \(m\) の 3 つの量子数によって特徴付けられます。これらの量子数は、軌道のエネルギーと形状を決定します。

エネルギー準位と電子構成

多電子原子では、電子は主量子数 \(n\) で定義されるさまざまなエネルギーレベルに分布しています。によれば、電子は最初に最低エネルギー準位を満たす。パウリの排除原則そして、へフントの法則。原子の電子配置は、軌道内の電子の分布を表します。

注： :
パウリの排他原理は、2 つの電子が同じ 4 つの量子数 (n、l、ml、ms) を持つことを禁止しますが、フントの法則は、電子がペアになる前に平行スピンを持つ縮退軌道を占有することを予測します。

詳細説明: 炭素の軌道と電子

炭素 (\(Z = 6\)) には 6 つの電子があります。これらの電子は、量子力学の規則に従って原子軌道内に分布します。炭素の電子配置は次のとおりです。

\[ 1s^2 \、2s^2 \、2p^2 \]

これはつまり：

2電子\(1s\) 軌道 (最低エネルギー準位) を占めます。
2電子\(2s\) 軌道 (わずかに高いエネルギー準位) を占めます。
2電子\(2p\) 軌道 (さらに高いエネルギー準位) を占めます。

軌道 \(2p\): 3 つの異なる空間形状

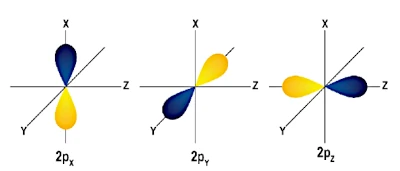
\(p\) 軌道には 3 つのタイプがあり、3 つの異なる空間方向に対応します。

\(p\) 軌道は、\(x\)、\(y\)、\(z\) 軸に沿った方向を向いた「ダンベル」形状 (またはローブ) を持っています。これら 3 つの軌道は互いに直交しています。これは、これらが空間の異なる領域を占有することを意味します。

軌道 \(p_x\): \(x\) 軸に沿って配置されます。
軌道 \(p_y\): \(y\) 軸に沿って整列します。
軌道 \(p_z\): \(z\) 軸に沿って整列します。

これら 3 つの \(p\) 軌道は縮退しています。つまり、同じエネルギーを持っています。カーボンの場合は、2電子残りはこれらの軌道 \(2p\) に分布します。によると、フントの法則, 電子は、ペアになる前に、まず平行スピンを持つ個別の \(p\) 軌道を占めます。したがって、炭素の場合は次のようになります。

電子は \(p_x\) 軌道を占めます。
電子は \(p_y\) 軌道を占めます。
\(p_z\) 軌道は空のままです。

カーボンの場合は、2電子\(2p\) 軌道は、利用可能な 3 つの軌道 (\(p_x\) と \(p_y\)) のうち 2 つを占め、3 つ目 (\(p_z\)) は空のままになります。これは、電子が空間内に均一に分布しているのではなく、原子軌道によって定義される特定の領域を占めていることを示しています。この分布は、特定の方向に共有結合を形成する能力など、炭素の化学的特性を理解するために不可欠です。

スクリーニング効果と有効エネルギー

多電子原子では、内部電子が部分的に原子核の正電荷を外部電子から「遮蔽」します。この遮蔽効果は、外部電子に対する原子核の効果的な引力を減少させ、そのエネルギーに影響を与えます。電子が感じる有効エネルギーは次の式で近似できます。

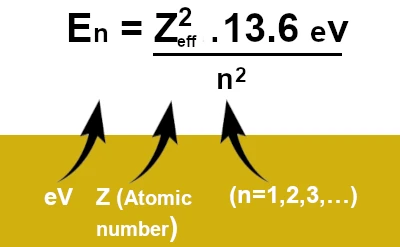
\[E_n = -\frac{Z_{\text{eff}}^2 \cdot 13.6 \, \text{eV}}{n^2}\]

ここで、 \(Z_{\text{eff}}\) はスクリーニング効果を考慮した原子核の実効電荷、 \(n\) は主量子数です。この式は、電子のエネルギーが原子核からの平均距離と感じられる有効電荷に依存することを示しています。

\(2p\) 軌道内の電子のエネルギーの計算

\(2p\) 軌道内の電子のエネルギーは水素化原子モデルを使用して推定できますが、このモデルは炭素のような多電子原子を簡略化したものです。主量子数 \(n\) の軌道内の電子のエネルギー \(E_n\) は、次の式で与えられます。

\[E_n = -\frac{Z_{\text{eff}}^2 \cdot R_H}{n^2}\]

または：

\(Z_{\text{eff}}\) は電子が感じる有効核電荷です。
\(R_H\) はリュードベリ定数 (\(R_H \約 13.6 \, \text{eV}\))、
\(n\) は主量子数です。

炭素の \(2p\) 殻内の電子の場合、 \(n = 2\) です。炭素の \(2p\) 電子の有効核電荷 \(Z_{\text{eff}}\) は約 \(3.14\) です (この値は計算モデルによって異なる場合があります)。したがって、 \(2p\) 軌道内の電子のエネルギーは次のようになります。

\[E_{2p} = -\frac{(3.14)^2 \cdot 13.6 \, \text{eV}}{2^2} \約 -30.6 \, \text{eV}\]

このエネルギーは \(1s\) (E1s≈−489.6eV) および \(2s\) (E2s≈−35.1eV) 軌道の電子のエネルギーよりも高く、これが \(2p\) 電子が原子核にそれほど強く結合しない理由を説明しています。

-30.6eV が -489.6eV より「高い」のはなぜですか?

原子内の電子のエネルギーは、原子に対する相対的に測定されます。基準状態これは一般に自由電子 (つまり、原子核に結合しなくなった電子) のエネルギーです。慣例により、自由電子のエネルギーは0 eVとして定義されます。負のエネルギーとは、電子が原子核に結合していることを意味します。エネルギーが負であるほど、電子は原子核に強く結合します。 -30.6eV は数値的には -489.6eV よりも大きいですが、それほど負ではありません。これは、2p 軌道の電子のエネルギーが 1s 軌道の電子のエネルギーよりもゼロに近いことを意味します。