ソーラーパネルはどのようにして電力網に電力を供給するのでしょうか?

同期インバータ: 電力網にエネルギーを伝送する秘密 — Description of the Blue curve: Supplier network, Red curve: Photovoltaic inverter slightly ahead of phase, Orange zone: moments when the inverter has a higher pressure, therefore active current injection. Result: energy flows in the right direction.画像出典:astronoo.com （新しいウィンドウ）

基本的な概念: 電流と電位の差

あ太陽光発電パネル家庭内設備 (および供給業者のネットワーク) に接続された直流電圧 (DC) は、インバーターによって同期された交流電圧 (AC) に変換されます。この電圧は、同じ周波数 (50 Hz) とネットワークの振幅に匹敵する振幅に設定されます。

電気では、次の場合にのみ電流が流れます。潜在的な差がある場合(ΔV) — 特に直流では、瞬間的な電圧差のみが電流の流れを決定します。一方、同期した 2 つの交流電源 (同じ周波数、同じ波形) の場合、正弦波間の位相ずれ (数度) のおかげで、瞬間的な電圧が等しくなる場合でも、電流が流れることができます。

この文脈では、それは電圧間の位相差、同様に回路インピーダンス特性、電流の存在と方向を決定します。

注：:
220 V の交流電圧では、電圧は +311 V から -311 V まで変化します。実際、220 V の値は交流電圧の実効値 (RMS) です。電力計算や電気機器の仕様に使用される値です。 AC 電圧は、正の最大値と負の最大値の間で振動します。実際の最大値（振幅）は \( V_{\mathrm{CRETE}} = V_{\mathrm{RMS}} \times \sqrt{2} \) → \( 220 \times \sqrt{2} \about 311\,\text{V} \) です。

エネルギー伝達における位相シフトの役割

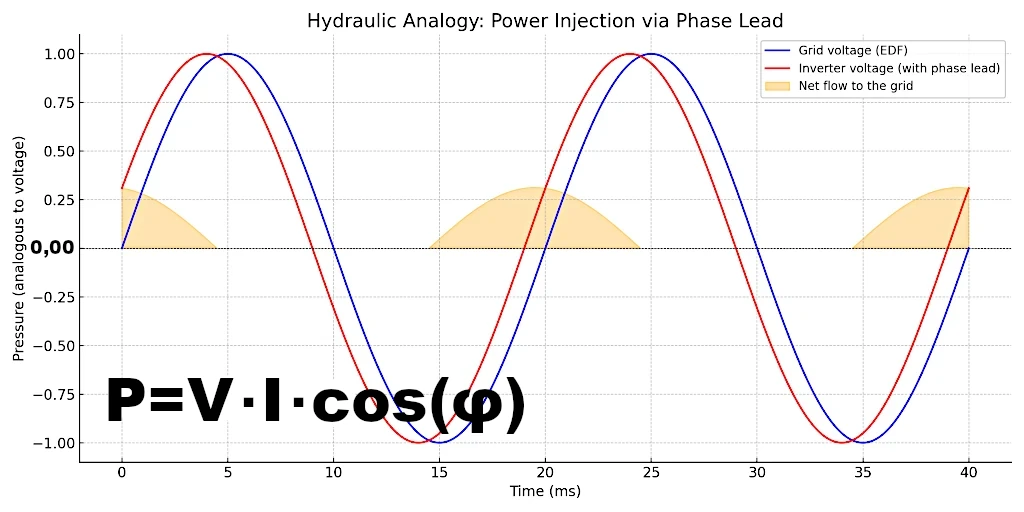
物理学の観点から見ると、この伝達はべき乗方程式 \( P = V \cdot I \cdot \cos(\varphi) \) に従います。この式は「単相正弦波 AC 有効電力の式」として知られています。

P は有効電力 (ワット、W)、
V は実効電圧 (ボルト、V)、
I は実効電流 (アンペア、A)、
cos(φ) は力率で、φ は電圧と電流の間の位相シフトです。

たとえ実効電圧が名目上同じ (たとえば 230 V) であっても、インバータがネットワークに向けて電流を注入できるのは、瞬間的な電圧変動 (位相、ダイナミクス、微調整) です。

可変圧力の 2 本の水道管との類似

同じパイプの両端に接続された 2 つの油圧ポンプが、それぞれ 50 Hz の周波数で圧力変動を生成することを想像してください。

これらの変化により、流体内に圧力波 (音波と同様) が発生し、パイプ内を伝わります。これらの波は、全体的な質量の移動を伴わずに、水の粒子の局所的な振動を伴い、流体の圧縮および緩和のゾーンを引き起こします。

このシステムは、電気回路内の 2 つの交流電圧源によく似ています。圧力は電圧を表し、流れは電流に対応し、流れに対する抵抗は電気インピーダンスに似ています。

ケース 1: 0° 位相シフト (完全に同位相でポンピング)

2 つの圧力は常に同じです。

共通パイプの両端間には圧力差がありません。

したがって、常に流量がゼロであり、流体の移動はありません。

\(Q(t) = 0 \)
\( \デルタ p(t) = 0 \)
瞬時電力: \( P(t) = \Delta p(t) \cdot Q(t) = 0 \)
平均パワー: 0

結論：エネルギー伝達はありません。圧力が振動しているにもかかわらず、流体は静的です。

ケース 2: 180° 位相シフト (ポンプの位相が逆)

相反する圧力：一方が押すと、もう一方は弱くなる。

各瞬間の最大圧力差。

流体は、一方のポンプからもう一方のポンプへと交互に強く振動します。

流量 \(Q(t)\) は圧力差と逆位相になります。

積 \( \Delta p(t) \cdot Q(t) \) は、半分の時間は負で、残りの半分は正ですが、完全に対称です。

結論：

瞬時電力: 変動し、プラスの場合もあれば、マイナスの場合もあります。
平均電力: ゼロ — エネルギーの周期的な交換 (コンデンサーやコイルなど) はありますが、正味の伝達はありません。
エネルギーの蓄積と放出が交互に行われます。

ケース 3: 90° 位相シフト (位相直交ポンプ)

一方のポンプが最大圧力にあるとき、もう一方のポンプは最大流量になります（圧力勾配が変化しているため）。

圧力と流量は直角位相（90°オフセット）です。

これは、瞬時電力が常にゼロではないが、サイクル中に符号が変化する状況に対応します。

結論：

瞬間パワー: 正弦波、注入と吸収が交互に行われます。
平均パワー: 常にゼロ - 180° の場合と同様に、エネルギーが交互に伝達され、正味の蓄積はありません。

ケース 4: 中間位相シフト (例: 5°)

この場合、位相シフトは完全にゼロ（0°の場合のように）でも、90°（圧力と流量が最大オフセットにあるが正味伝達がない場合）でも、最大（180°の場合のように）でもありませんが、中間です。

圧力差は永続的に最大になるわけではなく、部分的に変化します。

流量も正弦波ですが、圧力と部分的に同位相になります。

この位相シフトにより、ポンプ間の正味のエネルギー伝達が生じ、その結果、一方のポンプからもう一方のポンプへの実際の流体の流れが生じます。

ポンプ A がポンプ B より進んでいる場合、エネルギーは A から B に伝達され、流体は平均して A から B に移動します。
ポンプ A の位相がずれている場合、エネルギーを A に伝達するのは B であり、流体は B から A に移動します。

位相シフトの関数としての電流注入
ケース番号	位相シフト (°)	圧力差	フロー \( Q(t) \)	インスタントパワー	平均電力
1	0°	ゼロ	ヌル	\(P(t) = 0 \)	0（転送なし）
2	90°	最大	圧力を加えた求積法で	正弦波、符号の交互	0（相互転送）
3	180°	最大	圧力に反対する	対称正弦波	0（相互転送）
4	中級（例：5年生）	部分的だがゼロではない	圧力に部分的に同調	正弦波のゼロ以外の平均値	≠ 0 (正味エネルギー伝達)

とはいえ、代替瞬時流量あらゆる場合に存在しますが、正味物質移動位相シフトが部分的（0°、90°、または 180°とは異なる）の場合にのみ表示されます。

したがって、流体は機械エネルギーの伝達体であり、物質輸送ベクトルになる可能性がある正味エネルギー伝達の状況で。