ベイズ公式と人工知能

ベイズの公式

ベイズの公式は、ベイズの定理とも呼ばれ、別のイベント B がすでに発生していることを知っていて、イベント A の確率を計算できる数式です。

ベイズの公式: P(A|B) = (P(B|A) * P(A)) / P(B)

A は、確率を推定したいイベントです。
B は私たちがすでに知っている出来事です。
P(A|B) は、イベント B がすでに発生していると仮定して、イベント A が発生する確率です。
P(B|A) は、イベント A がすでに発生していると仮定して、イベント B が発生する確率です。
P(A) は、イベント A がイベント B とは独立して発生する確率です。
P(B) は、イベント B がイベント A とは独立して発生する確率です。

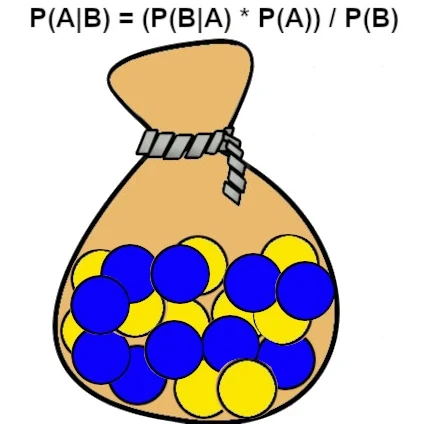
黄色のボールと青いボールが 10 個ずつ入った袋があるとします。 何も見ずにランダムにボールを引くと、それが黄色であることがわかります。
次に引くボールも黄色になる確率はどれくらいですか?

A: 次に描かれるボールは黄色です。
B: 最初に描かれたボールは黄色です。
P(A|B) = (P(B|A) * P(A)) / P(B)
P(B|A) = 10/20 = 0.5 (最初に引かれたボールが黄色であることを知っていて、黄色のボールを引く確率)
P(A) = 10/20 = 0.5 (黄色のボールを引く確率)
P(B) = 10/20 + 10/20 = 1 (黄色のボールを引く確率 + 青いボールを引く確率)
P(A|B) = (0.5 * 0.5) / 1 = 0.25
したがって、2 番目の黄色のボールを引く確率は 25% です。

ベイズ公式と人工知能

数学者トーマス・ベイズ牧師 (1702-1761) によって開発されたベイズの公式は、確率論と統計的推論 (母集団の標本から母集団についての結論を引き出すための一連の手法) の基本概念の 1 つです。

この公式の驚くべき点は、受け取った新しい情報に基づいて考えを変えることができるということです。 この公式は単純ですが、新しいことを学ぶにつれてアイデアがどのように進化するかを示しています。 言い換えれば、過去について知れば知るほど、未来をより正確に予測できるようになります。
この公式は、情報の蓄積によって予測を改良できることも示しています。 したがって、これは強力な意思決定ツールとなります。
異なる文脈で誕生しましたが、今日では人工知能 (AI) の分野でその完全な意味が見出されています。

1763 年、トーマス ベイズの友人であるリチャード プライス (1723-1791) は、「確率論の問題解決に向けたエッセイ」というタイトルの記事で彼の公式を発表しました。
ベイズの公式の中心である主観確率の概念は、当時物議を醸しました。 ベイズは彼の公式の正式な証明を提供しなかったため、数学者たちはそれを厳密ではないとして拒否しました。
その後、ピエール・シモン・ラプラス (1749-1827)、シメオン・ドゥニ・ポワソン (1781-1840) およびその他の数学者の研究によって、確率論の基礎が強化され、ベイズの公式がより現代的なものになりました。 現在、ベイズ公式は医学、金融、工学などの分野で広く使用されています。

人工知能は、人間の特定の認知能力を模倣できるコンピューター システムです。
機械学習と確率的推論は、ベイズの定理を特に利用する AI の 2 つの分野です。
機械学習のコンテキストでは、ベイズの公式は教師あり学習方法で使用され、特定のクラスが特定の観察の原因である確率を推定します。 たとえば、画像分類では、機械学習アルゴリズムはベイズ公式を使用して、画像内で観察された特徴に基づいて、特定の画像が犬ではなく猫である確率を推定できます。
さらに、ベイズの公式は、AI システムにおける意思決定への確率的アプローチであるベイズ推論の中心です。 固定されたトレーニング データに基づく頻度主義的なアプローチとは異なり、ベイズ推論では、新しいデータを観察すると確率的信念が更新されます。 これにより、特に複雑で動的な環境において、より適応的で堅牢な意思決定が可能になります。

死なない理論

250 年以上前に考案されたベイズ公式は、将来の不確実性から学ぶ方法です。 実際、それは信念を測定し、データの欠落や近似、さらには完全な無知からも学ぶことができることを教えてくれます。
したがって、それは科学が客観性と正確さを必要とするという信念に反します。 これは、この公式が当時の科学者によって廃止されたと宣言された理由を説明します。

この確率論は、コンピューターの登場によって、死にたくなかったが、広く実証されてきました。 これが人工知能アルゴリズムの唯一のロジックです。 ベイズの公式は、科学や技術のさまざまな分野で強力なツールとして機能し続けています。 ベイズ公式は、健全な統計原理と洗練されたコンピューター アルゴリズムを組み合わせることで、インテリジェントで適応性のある AI システムの構築において重要な役割を果たし続けます。