特殊相対性理論の方程式 (1905)

特殊相対性理論の公準

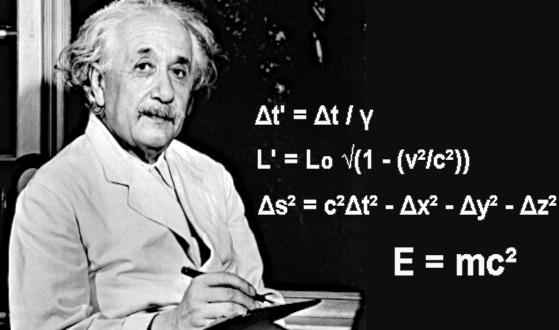
特殊相対性理論は、1905 年にアルバート アインシュタインによって定式化された物理理論です。 真空中の光の速度 (299,792,458 m/s) に近い高速度が存在する場合の物体の挙動や物理現象を扱います。

特殊相対性理論は 2 つの公準に基づいています。
- 相対性原理: 物理法則は、すべての慣性観測者 (相互に等速運動している観測者) にとって同じです。 優先リポジトリはありません。
- 光速度の一定性: 真空中の光速度は、光源や観察者の動きとは無関係に普遍的な定数です。 この速度は常に約 299,792,458 m/s、または特殊相対性理論の方程式の「c」に等しくなります。

特殊相対性理論の主な結果

• 時間の遅れは、時間の遅れとも呼ばれ、特殊相対性理論の重要な効果の 1 つです。 静止している観測者に対して相対的に動く時計は遅く見える。 高速で移動する物体では、「静止している」観測者に比べて時間の経過が遅くなります。
適切な時間の影響は次の式で表されます: Δt' = Δt / γ
- Δt' は、急速に移動する観測者によって測定された時間間隔です。
- Δt は、静止している観察者によって測定された時間間隔です。
- γ (ガンマ) は、γ = 1 / √(1 - (v²/c²)) として定義されるローレンツ係数です。ここで、「v」は物体の相対速度、「c」は真空中の光の速度です。

• ローレンツ収縮としても知られる長さの収縮は、特殊相対性理論によって予測される現象です。
物体が静止している観察者に対して高速で移動している場合、その観察者には物体がその移動方向に縮んで見えることになります。 高速で移動する物体は、静止している観察者から見ると、その移動方向に短縮して見える。
長さのローレンツ短縮は次の式で求められます: L' = L₀ * √(1 - (v²/c²))
- L' は、高速で移動する観測者によって測定された長さです。
- L₀ は適切な長さ (観察者が静止して測定した長さ)
- v はオブジェクトの相対速度です
- これは真空中での光の速度です。

• 時空間隔の不変性は、アルバート アインシュタインの特殊相対性理論の基本概念です。 これは、2 つのイベント間の時空間隔は、それらを観測するために選択された慣性基準が何であれ、不変のままである、つまり、すべての観測者にとって同じ値を持つという事実を表します。 2 つのイベント間の時空間間隔は、特定の基準枠内でこれらのイベントを隔てる空間間隔と時間間隔を組み合わせたものです。 特殊相対性理論では、Δs² と呼ばれる特定の計量を使用して時空間隔を定義します。 言い換えれば、時空間隔の不変性は、2 人の観測者が互いに対して一定の異なる速度で移動すると、同じイベントを隔てる時間と空間の異なる間隔を測定することを意味します。 ただし、これらの空間間隔と時間間隔を組み合わせた量 Δs² は、すべての観測者にとって同じになります。
時空間隔の不変性は、次の式で表されます。 Δs² = c²Δt² - Δx² - Δy² - Δz²
- Δs² は時空間隔です。
- それは真空中での光の速度です
- Δt は 2 つのイベント間の時間間隔です。
- Δx、Δy、Δz は 3 次元の空間間隔です。

• 質量エネルギーの等価性は特殊相対性理論の結果です。 それは、物体の質量はそのエネルギーの発現の一形態であり、逆にそのエネルギーは質量に変換できることを意味します。 言い換えれば、質量とエネルギーは実際には同じ物理量の 2 つの側面です。 質量とエネルギーの等価性は、有名な式 E=mc² で表されます。
- E は物体のエネルギーです
- m はその質量です
- これは真空中での光の速度です。

E=mc²

E=mc2 は、すべての物理学において最もよく知られ、最も人気のある方程式です。これは、1905 年 6 月 30 日の「運動中の物体の電気力学について」というタイトルの記事から 7 年後の 1912 年にアルバート アインシュタインのメモに登場しました。 この 1905 年の論文には、後に「特殊相対性理論」と呼ばれることになるものの基礎が含まれています。
E=mc² は現代物理学における最も革新的な発見の 1 つであり、宇宙の理解に大きな影響を与えました。
特殊相対性理論の方程式は、時間、空間、エネルギーが物体の急速な運動によってどのような影響を受けるかを示しています。
特殊相対性理論は何度も実験的に確認されており、光速に近い速度で高速移動する物体の挙動を記述するための強力かつ正確な理論であることが証明されています。 これは現代物理学の重要な柱を構成し、より一般的な一般相対性理論への道を開きました。