Letzte Aktualisierung: 3. August 2023

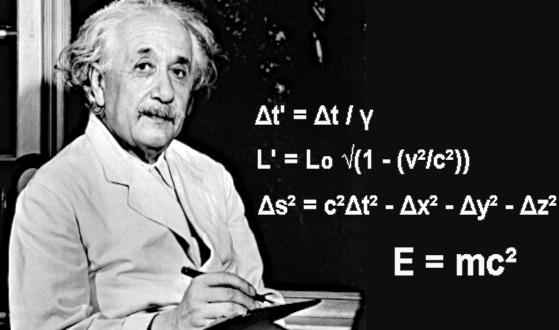
Die Gleichungen der speziellen Relativitätstheorie (1905)

Beschreibung des Bildes: Albert Einstein (1879-1955) ist ein theoretischer Physiker und Nobelpreisträger für Physik (1921) für die Korpuskularnatur des Lichts für die Erforschung des photoelektrischen Effekts.

Die Postulate der speziellen Relativitätstheorie

Die Spezielle Relativitätstheorie ist eine physikalische Theorie, die 1905 von Albert Einstein formuliert wurde. Es befasst sich mit dem Verhalten von Objekten und physikalischen Phänomenen bei hohen Geschwindigkeiten, nahe der Lichtgeschwindigkeit im Vakuum (299.792.458 m/s).

Die Spezielle Relativitätstheorie basiert auf zwei Postulaten:
- Das Relativitätsprinzip: Die Gesetze der Physik gelten für alle Inertialbeobachter (Beobachter in gleichförmiger Bewegung relativ zueinander). Es gibt kein bevorzugtes Repository.
- Die Konstanz der Lichtgeschwindigkeit: Die Lichtgeschwindigkeit im Vakuum ist eine universelle Konstante, unabhängig von der Bewegung der Lichtquelle und des Beobachters. Diese Geschwindigkeit beträgt immer ungefähr 299.792.458 m/s oder „c“ in den Gleichungen der Speziellen Relativitätstheorie.

Die wichtigsten Konsequenzen der Speziellen Relativitätstheorie

• Zeitdilatation, auch Zeitdilatation genannt, ist einer der Schlüsseleffekte der speziellen Relativitätstheorie. Uhren, die sich relativ zu einem ruhenden Beobachter bewegen, scheinen langsamer zu werden. Die Zeit vergeht bei einem sich schnell bewegenden Objekt langsamer als bei einem „stationären“ Beobachter.
Der Effekt der Eigenzeit wird in der Formel ausgedrückt: Δt' = Δt / γ
- Δt' ist das von einem sich schnell bewegenden Beobachter gemessene Zeitintervall
- Δt ist das von einem ruhenden Beobachter gemessene Zeitintervall
- γ (Gamma) ist der Lorentz-Faktor, definiert als γ = 1 / √(1 - (v²/c²)), wobei „v“ die relative Geschwindigkeit des Objekts und „c“ die Lichtgeschwindigkeit im Vakuum ist.

• Längenkontraktion, auch Lorentz-Kontraktion genannt, ist ein von der speziellen Relativitätstheorie vorhergesagtes Phänomen.
Wenn sich ein Objekt relativ zu einem ruhenden Beobachter mit hoher Geschwindigkeit bewegt, sieht dieser Beobachter, wie sich das Objekt in seiner Bewegungsrichtung zusammenzieht. Sich schnell bewegende Objekte scheinen sich in ihrer Bewegungsrichtung zu verkürzen, wenn sie von einem ruhenden Beobachter betrachtet werden.
Die Lorentz-Kontraktion für die Länge ergibt sich aus der Formel: L' = L₀ * √(1 - (v²/c²))
- L' ist die von einem sich schnell bewegenden Beobachter gemessene Länge
- L₀ ist die richtige Länge (von einem ruhenden Beobachter gemessene Länge)
- v ist die relative Geschwindigkeit des Objekts
- das ist die Lichtgeschwindigkeit im Vakuum.

• Raum-Zeit-Intervallinvarianz ist ein grundlegendes Konzept der speziellen Relativitätstheorie von Albert Einstein. Es drückt die Tatsache aus, dass das Raum-Zeit-Intervall zwischen zwei Ereignissen unabhängig von der zu ihrer Beobachtung gewählten Trägheitsreferenz invariant bleibt, das heißt, dass es für alle Beobachter den gleichen Wert hat. Das Raum-Zeit-Intervall zwischen zwei Ereignissen ist eine Kombination aus den Raum- und Zeitintervallen, die diese Ereignisse in einem bestimmten Bezugsrahmen trennen. In der speziellen Relativitätstheorie verwenden wir eine bestimmte Metrik, um das Raum-Zeit-Intervall zu definieren, das als Δs² bezeichnet wird. Mit anderen Worten bedeutet Raum-Zeit-Intervall-Invarianz, dass zwei Beobachter, die sich relativ zueinander mit konstanter und unterschiedlicher Geschwindigkeit bewegen, unterschiedliche Zeit- und Raumintervalle messen, die dieselben Ereignisse trennen. Die Größe Δs², die diese Raum- und Zeitintervalle zusammenfasst, wird jedoch für alle Beobachter gleich sein.
Die Invarianz des Raum-Zeit-Intervalls wird in der Formel ausgedrückt: Δs² = c²Δt² - Δx² - Δy² - Δz²
- Δs² ist das Raum-Zeit-Intervall
- es ist die Lichtgeschwindigkeit im Vakuum
- Δt ist das Zeitintervall zwischen den beiden Ereignissen
- Δx, Δy und Δz sind die Raumintervalle in drei Dimensionen.

• Masse-Energie-Äquivalenz ist eine Folge der speziellen Relativitätstheorie. Das bedeutet, dass die Masse eines Objekts eine Form der Manifestation seiner Energie ist und dass umgekehrt Energie in Masse umgewandelt werden kann. Mit anderen Worten: Masse und Energie sind eigentlich zwei Aspekte derselben physikalischen Größe. Die Masse-Energie-Äquivalenz wird in der berühmten Formel E=mc² ausgedrückt.
- E ist die Energie eines Objekts
- m ist seine Masse
- das ist die Lichtgeschwindigkeit im Vakuum.

E=mc²

E=mc2 ist die bekannteste und beliebteste Gleichung der gesamten Physik. Es erschien 1912 in einer Notiz von Albert Einstein, sieben Jahre nach dem Artikel vom 30. Juni 1905 mit dem Titel „Über die Elektrodynamik bewegter Körper“. Dieses Papier aus dem Jahr 1905 enthält die Grundlage dessen, was später als „Theorie der Speziellen Relativitätstheorie“ bezeichnet wurde.
E=mc² war eine der revolutionärsten Entdeckungen der modernen Physik und hatte einen erheblichen Einfluss auf unser Verständnis des Universums.
Die Gleichungen der Speziellen Relativitätstheorie zeigen, wie Zeit, Raum und Energie durch die schnellen Bewegungen von Objekten beeinflusst werden.
Die Spezielle Relativitätstheorie wurde mehrfach experimentell bestätigt und hat sich als starke und genaue Theorie zur Beschreibung des Verhaltens sich schnell bewegender Objekte mit Geschwindigkeiten nahe der Lichtgeschwindigkeit erwiesen. Sie stellt eine wesentliche Säule der modernen Physik dar und ebnete den Weg zur allgemeineren Relativitätstheorie.