Beschreibung des Bildes: Die von einer Oberfläche aufgenommene Sonnenenergie hängt vom Einfallswinkel der Sonnenstrahlen im Verhältnis zu dieser Oberfläche ab.
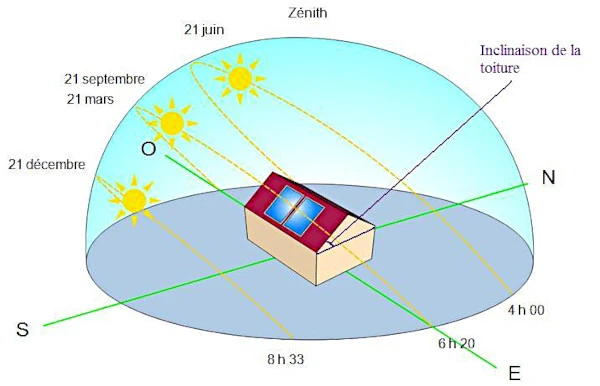
Das Lambertsche Gesetz (Johann Heinrich Lambert 1728-1777) besagt, dass die Intensität der einfallenden Sonnenenergie I auf einer Oberfläche proportional zum Kosinus des Einfallswinkels θ zwischen dem Sonnenstrahl und der Normalen zur Oberfläche ist: I = I0 cos(θ)
ICH0ist die Intensität der Sonnenenergie senkrecht zur Oberfläche, also die Lichtintensität in Watt pro Quadratmeter (W/m²).
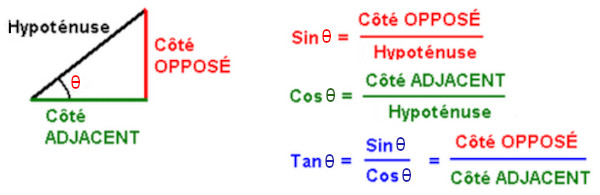
Der Kosinus eines Winkels in einem rechtwinkligen Dreieck ist das Verhältnis der Länge der an den Winkel angrenzenden Seite zur Länge der Hypotenuse.
θ ist der Einfallswinkel relativ zur Erdoberfläche. Der Einfallswinkel wird durch die relative Position der Sonne in Bezug auf die jeweilige Oberfläche bestimmt. Im Allgemeinen variiert dieser Winkel je nach Breitengrad, Tag des Jahres und Tageszeit. Bei einer horizontalen Fläche wird der Einfallswinkel auch durch den Sonnenhöhenwinkel (Sonnenhöhe) und den Sonnenazimut beeinflusst.
Für eine flache, geneigte Oberfläche kann die empfangene Sonnenenergie durch Integration der Intensität der Sonnenenergie über die Oberfläche berechnet werden. Wenn E die pro Flächeneinheit empfangene Energie in Joule (J) ist: E = E0 cos(θ) (E0ist die Energie, die pro Flächeneinheit empfangen wird, wenn die Strahlen senkrecht stehen).
Der Zusammenhang zwischen Energie E und Intensität I zeigt, dass die von einer Oberfläche aufgenommene Gesamtenergie proportional zur Lichtintensität, der Oberfläche und der Belichtungszeit ist.
I = E/A.t
I ist die Lichtintensität in Watt pro Quadratmeter (W/m²).
E ist die Energie in Joule (J).
A ist die Fläche in Quadratmetern (m²).
t ist die Zeit in Sekunden (s).
Wie groß ist die Sonnenenergie, die von einer Oberfläche empfangen wird, wenn der Einfallswinkel (relativ zur Vertikalen) θ = 30 Grad beträgt?
Intensität der Sonnenenergie senkrecht zur Oberfläche, I0 = ≈ 1000 W/m², auch Solarkonstante genannt (dies ist ein typischer Wert für klaren Himmel am Sonnenmittag).
Ich = Ich0 cos(θ)
cos(30°) = √²/2 ≈ 0,866
I = 1000 W/m² x 0,866 ≈ 866 W/m² oder 86 % der Solarkonstante.
Wie groß ist die Sonnenenergie, die eine Oberfläche empfängt, wenn der Einfallswinkel θ = 45 Grad beträgt?
Ich = Ich0 cos(θ)
cos(45°) = √²/2 ≈ 0,707
I = 1000 W/m² x 0,707 ≈ 707 W/m² oder 70 % der Solarkonstante.
Wie groß ist die Sonnenenergie, die eine Oberfläche empfängt, wenn der Einfallswinkel θ = 90 Grad beträgt?
Ich = Ich0 cos(θ)
cos(90°) = 0
I = 1000 W/m² x 0 ≈ 0 W/m².
• Bei 30 Grad erhält die Oberfläche ≈ 866 W/m².
• Bei 45 Grad erhält die Oberfläche ≈ 707 W/m².
• Bei 66 Grad erhält die Oberfläche ≈ 406 W/m².
• Bei 90 Grad erhält die Oberfläche 0 W/m².
Das photoelektrische Effekt verstehen: Licht und Elektronen 
Wie weit ist der Horizont entfernt? 
Wie speisen Solarmodule Strom ins Netz ein? 
Impulsdynamik zur Erklärung des Antriebs von Raketen oder Quallen 
Energieverteilung der Elektronen in Atomen 
Heisenbergs Unschärferelation: Quantenunsicherheit verstehen 
Zusammenhang zwischen Energie, Leistung und Zeit 
Warum gibt es eine Grenze für Kälte, aber nicht für Wärme? 
Galileis Fallgesetz 
Das Gesetz der idealen Gase 
Schrödingergleichung und Atomstruktur 
Noethers Theorem: Energieerhaltung aus Symmetrien 
Verhältnis zwischen schwerer und träger Masse und das Äquivalenzprinzip 
Die dritte grundlegende Gleichung der Physik 
Die zweite grundlegende Gleichung der Physik 
Die erste grundlegende Gleichung der Physik 
Die elektromagnetische Kraft oder Lorentzkraft 
Die empfangene Sonnenenergie variiert mit der Neigung 
Warum ist Marmor kälter als Holz? 
Warum hat ein Photon ohne Masse Energie? 
Bayes-Formel und künstliche Intelligenz 
Die sieben fundamentalen Konstanten der Physik 
Welche Temperatur herrscht im interstellaren Raum? 
Strahlungskurven des schwarzen Körpers: Plancks Gesetz 
Das Äquivalenzprinzip: Gravitationseffekte sind von Beschleunigungen nicht unterscheidbar 
E=mc²: Die vier fundamentalen Konzepte des Universums überdacht 
Wie wiegt man die Sonne? 
Gleichung des freien Falls (1604) 
Coulomb-Gleichung (1785) 
Boltzmann-Gleichung zur Entropie (1877) 
Gleichungen der speziellen Relativität (1905) 
Gleichung der allgemeinen Relativität (1915) 
Gleichungen der Planetenrotation: Zwischen Drehimpuls und gravitativer Balance 
Gleichung der Orbitgeschwindigkeit eines Planeten 
Plancks Gleichung 
Schrödingergleichung 
Wie beschreiben Newtons drei Gesetze die gesamte klassische Mechanik? 
Maxwells Gleichungen 
Dirac-Gleichung 
Energieerhaltung 
Gleichung der elektromagnetischen Induktion 
Warum haben Elementarteilchen keine Masse? 
Unterschied zwischen Wärme und Temperatur