Energieverteilung von Elektronen in polyelektronischen Atomen

Bildbeschreibung: Elektronen besetzen bestimmte Orbitale, die durch Quantenzahlen definiert sind, und ihre Energie hängt von ihrer Position im Atom ab. Bildquelle:astronoo.com

Einführung in die Elektronenenergie

L'Elektronenenergiein einempolyelektronisches Atomist ein zentrales Konzept der Quantenmechanik. Anders als das Wasserstoffatom, das nur ein Elektron hat, enthalten polyelektronische Atome mehrere Elektronen, die miteinander und mit dem Kern interagieren. Diese komplexen Wechselwirkungen erschweren die Berechnung der elektronischen Energie, sind aber für das Verständnis der chemischen und physikalischen Eigenschaften der Elemente unerlässlich.

Die Energie des Elektrons ermöglicht es uns, den atomaren Aufbau und die Eigenschaften von Elementen zu verstehen. Die Schrödinger-Gleichung, Atomorbitale und Abschirmeffekte spielen eine Schlüsselrolle bei der Bestimmung der Energieniveaus und der elektronischen Konfiguration.

Schrödingers Gleichung und Atomorbitale

Die Energie der Elektronen in einem Atom wird beschrieben durchSchrödinger-Gleichung, eine Grundgleichung der Quantenmechanik. Für ein polyelektronisches Atom lautet die Schrödinger-Gleichung:

\[ \hat{H} \Psi = E \Psi \]

Dabei ist \(\hat{H}\) der Hamilton-Operator, \(\Psi\) die Wellenfunktion des Elektrons und \(E\) die diesem Zustand zugeordnete Energie. Der Hamilton-Operator umfasst die Begriffe kinetische Energie und potentielle Energie, wobei letztere die Wechselwirkungen zwischen den Elektronen und dem Kern sowie die Wechselwirkungen zwischen den Elektronen selbst berücksichtigt.

Die Lösung dieser Gleichung ergibt dieAtomorbitale, die die beschreibenräumliche Verteilung der Elektronen um den Kern. Jedes Orbital ist durch drei Quantenzahlen gekennzeichnet: die Hauptquantenzahl \(n\), die azimutale Quantenzahl \(l\) und die magnetische Quantenzahl \(m\). Diese Quantenzahlen bestimmen die Energie und Form der Orbitale.

Energieniveaus und elektronische Konfiguration

In einem polyelektronischen Atom sind die Elektronen auf verschiedene Energieniveaus verteilt, die durch die Hauptquantenzahl \(n\) definiert sind. Elektronen füllen demnach zuerst die niedrigsten EnergieniveausPauli-Ausschlussprinzipund zumHunds Regel. Die elektronische Konfiguration eines Atoms beschreibt die Verteilung der Elektronen in Orbitalen.

Hinweis: :
Das Pauli-Ausschlussprinzip verbietet, dass zwei Elektronen die gleichen vier Quantenzahlen (n, l, ml, ms) haben, während die Hundsche Regel vorhersagt, dass Elektronen vor der Paarung entartete Orbitale mit parallelen Spins besetzen.

Ausführliche Erklärung: Orbitale und Elektronen im Kohlenstoff

Kohlenstoff (\(Z = 6\)) hat 6 Elektronen. Diese Elektronen werden nach den Regeln der Quantenmechanik in Atomorbitalen verteilt. Die elektronische Konfiguration von Kohlenstoff ist:

\[ 1s^2 \, 2s^2 \, 2p^2 \]

Das heisst:

• 2 Elektronenbesetzen das \(1s\)-Orbital (niedrigstes Energieniveau).
• 2 Elektronenbesetzen das \(2s\)-Orbital (etwas höheres Energieniveau).
• 2 Elektronenbesetzen die \(2p\)-Orbitale (noch höheres Energieniveau).

Orbitale \(2p\): Drei unterschiedliche räumliche Formen

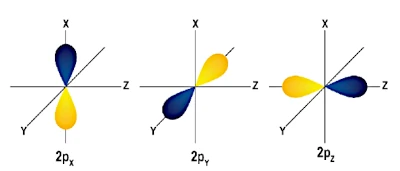
Es gibt drei Arten von \(p\)-Orbitalen, die drei unterschiedlichen räumlichen Orientierungen entsprechen:

Die \(p\)-Orbitale haben „Hantel“-Formen (oder Lappen), die entlang der \(x\), \(y\)- und \(z\)-Achsen ausgerichtet sind. Diese drei Orbitale sind orthogonal zueinander, was bedeutet, dass sie unterschiedliche Bereiche des Raums einnehmen.

1. Orbital \(p_x\): entlang der \(x\)-Achse ausgerichtet.
2. Orbital \(p_y\): entlang der \(y\)-Achse ausgerichtet.
3. Orbital \(p_z\): entlang der \(z\)-Achse ausgerichtet.

Diese drei \(p\)-Orbitale sind entartet, haben also die gleiche Energie. Im Fall von Kohlenstoff ist das2 ElektronenDie übrigen sind in diesen Orbitalen \(2p\) verteilt. Laut derHunds Regel, Elektronen besetzen vor der Paarung zunächst unterschiedliche \(p\)-Orbitale mit parallelen Spins. Also für Kohlenstoff:

• Ein Elektron besetzt das \(p_x\)-Orbital.
• Ein Elektron besetzt das \(p_y\)-Orbital.
• Das \(p_z\)-Orbital bleibt leer.

Im Fall von Kohlenstoff ist das2 Elektronen\(2p\)-Orbitale besetzen zwei der drei verfügbaren Orbitale (\(p_x\) und \(p_y\)), während das dritte (\(p_z\)) leer bleibt. Dies zeigt, dass sich Elektronen nicht gleichmäßig im Raum verteilen, sondern bestimmte, durch Atomorbitale definierte Bereiche besetzen. Diese Verteilung ist wichtig für das Verständnis der chemischen Eigenschaften von Kohlenstoff, einschließlich seiner Fähigkeit, kovalente Bindungen in bestimmte Richtungen zu bilden.

Screening-Effekte und effektive Energie

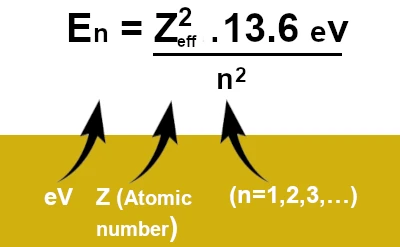
In einem polyelektronischen Atom „schirmen“ die inneren Elektronen teilweise die positive Ladung des Kerns für die äußeren Elektronen ab. Dieser Abschirmeffekt verringert die effektive Anziehungskraft des Kerns auf die äußeren Elektronen, was deren Energie beeinflusst. Die effektive Energie, die ein Elektron empfindet, kann durch die Formel angenähert werden:

\[E_n = -\frac{Z_{\text{eff}}^2 \cdot 13.6 \, \text{eV}}{n^2}\]

wobei \(Z_{\text{eff}}\) die effektive Ladung des Kerns unter Berücksichtigung des Abschirmeffekts und \(n\) die Hauptquantenzahl ist. Diese Formel zeigt, dass die Energie der Elektronen von ihrem durchschnittlichen Abstand vom Kern und der effektiv empfundenen Ladung abhängt.

Berechnung der Energie von Elektronen in \(2p\)-Orbitalen

Die Energie von Elektronen in \(2p\)-Orbitalen kann mithilfe des Hydrogenoid-Atommodells geschätzt werden, obwohl dieses Modell eine Vereinfachung für polyelektronische Atome wie Kohlenstoff darstellt. Die Energie \(E_n\) eines Elektrons in einem Orbital der Hauptquantenzahl \(n\) wird durch die Formel angegeben:

\[E_n = -\frac{Z_{\text{eff}}^2 \cdot R_H}{n^2}\]

Oder :

• \(Z_{\text{eff}}\) ist die effektive Kernladung, die das Elektron empfindet,
• \(R_H\) ist die Rydberg-Konstante (\(R_H \ca. 13,6 \, \text{eV}\)),
• \(n\) ist die Hauptquantenzahl.

Für die Elektronen in der \(2p\)-Schale von Kohlenstoff gilt \(n = 2\). Die effektive Kernladung \(Z_{\text{eff}}\) für die \(2p\)-Elektronen des Kohlenstoffs beträgt ungefähr \(3,14\) (dieser Wert kann je nach Berechnungsmodell variieren). Somit beträgt die Energie der Elektronen in den \(2p\)-Orbitalen:

\[E_{2p} = -\frac{(3.14)^2 \cdot 13.6 \, \text{eV}}{2^2} \ approx -30.6 \, \text{eV}\]

Diese Energie ist höher als die der Elektronen in den Orbitalen \(1s\) (E1s≈−489,6eV) und \(2s\) (E2s≈−35,1eV), was erklärt, warum die \(2p\)-Elektronen weniger stark an den Kern gebunden sind.

Im Fall von Kohlenstoff ist das2 Elektronen\(2p\)-Orbitale besetzen zwei der drei verfügbaren Orbitale (\(p_x\) und \(p_y\)), während das dritte (\(p_z\)) leer bleibt. Dies zeigt, dass sich Elektronen nicht gleichmäßig im Raum verteilen, sondern bestimmte, durch Atomorbitale definierte Bereiche besetzen. Diese Verteilung ist wichtig für das Verständnis der chemischen Eigenschaften von Kohlenstoff, einschließlich seiner Fähigkeit, kovalente Bindungen in bestimmte Richtungen zu bilden.

Warum ist −30,6 eV „höher“ als −489,6 eV?

Die Energie der Elektronen in einem Atom wird relativ zu a gemessenReferenzzustand, was im Allgemeinen die Energie eines freien Elektrons ist (d. h. eines Elektrons, das nicht mehr an den Kern gebunden ist). Konventionell gilt:Die Energie eines freien Elektrons ist als 0 eV definiert. Negative Energie bedeutet, dass das Elektron an den Kern gebunden ist. Je negativer die Energie, desto stärker ist das Elektron an den Kern gebunden. Obwohl −30,6 eV numerisch größer als −489,6 eV ist, ist es weniger negativ. Das bedeutet, dass die Energie des Elektrons im 2p-Orbital näher bei Null liegt als die des Elektrons im 1s-Orbital.