Letzte Aktualisierung: 11. November 2024

Schrödingers Gleichung und ihre Rolle in der Atomstruktur

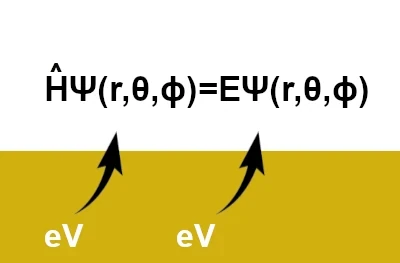
Schrödinger-Gleichung und Struktur der Atome

Bildbeschreibung: Die zeitunabhängige Schrödinger-Gleichung kann gelöst werden, um physikalische Werte wie die quantisierte Energie atomarer Zustände zu erhalten. Der Hamilton-Operator (Ĥ) ist besonders wichtig, da er die Gesamtenergie eines Quantensystems darstellt. Wenn wir diesen Operator auf eine Wellenfunktion anwenden, erhalten wir die diesem Zustand zugeordnete Energie. Das Gleichgewicht zwischen diesen beiden Begriffen bestimmt das Verhalten des Partikels. In der Atomphysik drücken wir Energie in Elektronenvolt aus, 1eV=1,602×10⁻¹⁹ Joule.

Struktur der Atome nach der Schrödinger-Gleichung

Die Schrödinger-Gleichung, die 1925 von Erwin Schrödinger (1887-1961) formuliert wurde, spielt eine zentrale Rolle beim Verständnis der Struktur von Atomen. Es ermöglicht die Beschreibung des Quantenzustands von Elektronen in einem Atom und die Bestimmung der Energieniveaus, die jeder elektronischen Schicht sowie den Unterschalen zugeordnet sind. Dieser Ansatz basiert auf der Quantenmechanik, die sich grundlegend von klassischen Beschreibungen unterscheidet.

Schrödingers Gleichung für das Atom

Die Lösung dieser Gleichung ermöglicht die Berechnung der diskreten Energieniveaus eines Atoms.

$$\hat{H} \Psi(r, \theta, \phi) = E \Psi(r, \theta, \phi)$$

$\hat{H}$ ist der Hamilton-Operator, der die darstelltGesamtenergiedes Quantensystems (kinetische Energie + potentielle Energie),
$\Psi(r, \theta, \phi)$ ist dasWellenfunktiondes Elektrons, die von den Kugelkoordinaten abhängt (R: Die radiale Koordinate,θ: Die Polarkoordinate,ϕ: Die azimutale Koordinate). Diese Funktion enthält alle Informationen über das System und seine Form und sein Verhalten werden zur Berechnung physikalischer Größen wie Energie, Wahrscheinlichkeit der Anwesenheit des Teilchens in einer bestimmten Region,
$E$ ist dasEnergie, die mit dem Quantenzustand verbunden istgegeben.

Hinweis: :
In der Quantenmechanik wird das Atom oft in Kugelkoordinaten beschrieben, da das Elektron eine sphärische Wahrscheinlichkeitsverteilung um den Kern herum aufweist. Sie sind sehr nützlich, um die Form und Ausrichtung von Atomorbitalen zu beschreiben.

Quantifizierte Energieniveaus

Die Energie des Elektrons imWasserstoffatome(Wasserstoff H⁺, Helium He⁺, Lithium Li²⁺, Beryllium Be³⁺usw.) quantifiziert wird. Die Energie hängt von Z und der Hauptquantenzahl n ab.

$$E_n = -13,6 \, \text{eV} \times \frac{Z^2}{n^2}$$

$E_n$ ist die Energie des $n$-Niveaus des Elektrons,
$n$ ist die Hauptquantenzahl ($n = 1, 2, 3, \dots$),
$13.6 \, \text{eV}$ ist die Ionisierungsenergie des Wasserstoffatoms,
$Z$ repräsentiert die Ordnungszahl eines chemischen Elements. Es gibt die Anzahl der Protonen im Kern eines Atoms an und bestimmt die Identität dieses Atoms.

Beispiele für Energiewerte für monoelektronische Ionen

DERMonoelektronen-Ionensind Ionen, die nur ein Elektron haben, alle anderen wurden entfernt. Diese Ionen werden häufig in theoretischen Modellen verwendet, um die Untersuchung ionisierter Systeme zu vereinfachen, in denen das Elektron in verschiedenen quantisierten Energieniveaus (mit möglichen Werten von n wie 1, 2, 3 usw.) zu finden ist.

Ionisierter Wasserstoff (H⁺): $E_n$=−13,6eV (da Z=1)
Ionisiertes Helium (He⁺): $E_n$=−54,4eV (da Z=2)
Ionisiertes Lithium (Li²⁺): $E_n$=−122,4eV (da Z=3)
Ionisiertes Beryllium (Be³⁺): $E_n$=−217,6eV (da Z=4)
Ionisiertes Bor (B⁴⁺): $E_n$=−340eV (da Z=5)
Ionisierter Kohlenstoff (C⁵⁺): $E_n$=−489,6eV (da Z=6)

Um das Wasserstoffatom zu ionisieren, also das Elektron freizusetzen, muss ihm eine Energie von mindestens 13,6 eV zugeführt werden, um diese Bindung aufzubrechen. Um das Kohlenstoffatom zu ionisieren, also das Elektron freizusetzen, muss ihm eine Energie von mindestens 489,6 eV zugeführt werden, um diese Bindung aufzubrechen. Dementsprechend ist die Energie umso negativer, je näher das Elektron am Kern ist.

Warum ist die Energie eines Elektrons in einem Atom negativ?

Negative Energie spiegelt in diesem Zusammenhang die Tatsache wider, dass das Elektron an das Atom gebunden ist und es ohne Zufuhr einer Energiemenge nicht verlassen kann. Die potentielle Energie ist negativ, da das Elektron vom Kern angezogen wird. Je näher das Elektron am Kern ist, desto negativer wird diese Energie (d. h. desto stabiler ist das Atom). Andererseits ist die kinetische Energie des Elektrons aufgrund des Zusammenhangs zwischen der Geschwindigkeit des Elektrons und der Kraft, die es auf seiner Umlaufbahn hält, ebenfalls negativ.

Anegative Energiezeigt an, dass das Elektron an den Kern gebunden ist und dass positive Energie (Ionisierungsenergie genannt) bereitgestellt werden muss, um es von ihm zu lösen.

Schichten und Unterschichten im Zusammenhang mit Orbitalen in der Atomstruktur

DERQuantenzahlensind Parameter, mit denen die Zustände eines Elektrons in einem Atom beschrieben werden. Es gibt vier Hauptgründe. Diese Quantenzahlen ermöglichen es, den Zustand eines Elektrons in einem Atom vollständig zu charakterisieren und seine Energieniveaus und seine Konfiguration im Raum zu bestimmen.

DERHauptquantenzahl n: Es beschreibt mehrere wichtige Eigenschaften von Elektronen in einem Atom, insbesondere ihre Energie und die Größe ihrer Umlaufbahn.
DERSekundärquantenzahl l: Es beschreibt die Form der Elektronenbahn. Es nimmt Werte von 0 bis $n-1$ an und bestimmt die Unterschichten (s, p, d, f usw.).
DERmagnetische Quantenzahl m_l: Es beschreibt die räumliche Ausrichtung der Umlaufbahn und nimmt Werte von $-l$ bis $+l$ an
DERSpinquantenzahl m_s: Es beschreibt die Ausrichtung des Spins des Elektrons und kann entweder $+1/2$ oder $-1/2$ sein

DERWindelnsind Mengen von Orbitalen mit derselben Hauptquantenzahl n.
DERUnterlagensind Teilmengen von Orbitalen mit demselben n und demselben l. Die Unterschalen werden daher durch die sekundäre Quantenzahl $l$ bestimmt.

Configuration électronique des coquilles et sous-coquilles
Shell (n)	Electrons / shell (2n²)	Subshell	Electrons / subshell	Orbitals / subshell
1	2	1s	2	1
2	8	2s 2p	2 6	1 3
3	18	3s 3p 3d	2 6 10	1 3 5
4	32	4s 4p 4d 4f	2 6 10 14	1 3 5 7

Examples of electronic structures:

Carbon (C, Z = 6) : 1s² 2s² 2p²
Sodium (Na, Z = 11) : 1s² 2s² 2p⁶ 3s¹
Potassium (K, Z = 19) : 1s² 2s² 2p⁶ 3s² 3p⁶ 4s¹

Abschluss

Die Schrödinger-Gleichung kann die Struktur von Atomen genau beschreiben, einschließlich der Energieniveaus der Elektronen in ihren Schalen und Unterschalen. Dieser Quantenansatz erklärt das Verhalten, das in den Emissions- und Absorptionsspektren von Elementen beobachtet wird, sowie die Anordnung von Elektronen um den Kern.