最終更新日: 2024 年 11 月 11 日

シュレディンガー方程式と原子構造におけるその役割

画像の説明: 時間に依存しないシュレーディンガー方程式を解くと、原子状態の量子化エネルギーなどの物理値を取得できます。ハミルトニアン演算子 (Ĥ) は、量子系の総エネルギーを表すため、特に重要です。この演算子を波動関数に適用すると、この状態に関連付けられたエネルギーが得られます。これら 2 つの項のバランスが粒子の動作を決定します。原子物理学では、エネルギーを電子ボルト、1eV=1.602×10で表します。⁻¹⁹ジュール。

シュレーディンガー方程式による原子の構造

シュレーディンガー方程式は、1925 年にエルヴィンシュレーディンガー (1887-1961) によって表現され、原子の構造を理解する上で中心的な役割を果たします。これにより、原子内の電子の量子状態を記述し、各電子層およびサブシェルに関連するエネルギー準位を決定することが可能になります。このアプローチは量子力学に基づいており、古典的な記述とは根本的に異なります。

原子のシュレディンガー方程式

この方程式を解くと、原子の離散エネルギー準位を計算できます。

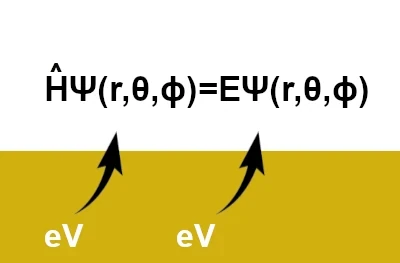
$$\hat{H} \Psi(r, \theta, \phi) = E \Psi(r, \theta, \phi)$$

$\hat{H}$ は、を表すハミルトニアンです。総エネルギー量子系 (運動エネルギー + 位置エネルギー)、
$\Psi(r, \theta, \phi)$ は波動関数電子の球座標に依存します (r: 動径座標、θ: 極座標、ϕ: 方位座標)。この関数にはシステムに関するすべての情報が含まれており、その形状と動作は、エネルギー、特定の領域における粒子の存在確率、
$E$ は量子状態に関連するエネルギー与えられた。

注： :
量子力学では、電子は原子核の周りに球状の確率分布を持っているため、原子は球状座標で記述されることが多く、原子軌道の形状と方向を記述するのに非常に役立ちます。

定量化されたエネルギーレベル

その中の電子のエネルギーは、水素原子(水素H⁺、ヘリウム He⁺、リチウム李²⁺、ベリリウム³⁺、など）を数値化します。エネルギーは Z と主量子数 n に依存します。

$$E_n = -13.6 \, \text{eV} \times \frac{Z^2}{n^2}$$

$E_n$ は電子の $n$ 準位のエネルギーであり、
$n$ は主量子数 ($n = 1, 2, 3, \dots$)、
$13.6 \, \text{eV}$ は水素原子のイオン化エネルギー、
$Z$ は化学元素の原子番号を表します。これは原子核内の陽子の数を示し、その原子の正体を決定します。

単電子イオンのエネルギー値の例

ザ単電子イオン電子を 1 つだけ持ち、他の電子はすべて取り除かれたイオンです。これらのイオンは、イオン化システムの研究を簡素化するために理論モデルでよく使用されます。電子はさまざまな量子化エネルギーレベル (1、2、3 などの n の値が考えられます) で見つけることができます。

イオン化水素 (H⁺): $E_n$=−13.6eV (Z=1 のため)
イオン化ヘリウム (He⁺): $E_n$=−54.4eV (Z=2 のため)
イオン化リチウム (Li²⁺): $E_n$=−122.4eV (Z=3 のため)
イオン化ベリリウム (Be³⁺): $E_n$=−217.6eV (Z=4 のため)
イオン化ホウ素 (B⁴⁺): $E_n$=−340eV (Z=5 のため)
イオン化炭素 (C⁵⁺): $E_n$=−489.6eV (Z=6 のため)

水素原子をイオン化する、つまり電子を放出するには、この結合を切断するために少なくとも 13.6 eV のエネルギーを水素原子に与える必要があります。炭素原子をイオン化する、つまり電子を放出するには、この結合を切断するために少なくとも 489.6 eV のエネルギーを炭素原子に与える必要があります。したがって、電子が原子核に近づくほど、エネルギーはより負になります。

原子内の電子のエネルギーはなぜ負なのでしょうか?

この文脈における負のエネルギーは、電子が原子に結合しており、一定量のエネルギーが供給されないと原子から逃げることができないという事実を反映しています。電子は原子核に引き寄せられるため、位置エネルギーは負になります。電子が原子核に近づくほど、このエネルギーはより負になります（つまり、原子はより安定します）。一方、電子の運動エネルギーも、電子の速度と電子をその軌道上に維持する力との関係により負になります。

あ負のエネルギー電子が原子核に結合しており、電子を原子核から引き離すには正のエネルギー (イオン化エネルギーと呼ばれる) を提供する必要があることを示します。