最終更新日: 2025 年 10 月 10 日

惑星の公転速度の方程式

太陽系の惑星の公転速度の図 — 太陽の周りの惑星軌道の概略図。
画像出典:astronoo.com

軌道速度の定義

そこには軌道速度惑星の速度は、その星の周りの軌道に沿って移動する速度です。それは次のバランスから生まれます。重力そして遠心力。円軌道の動的平衡条件では、向心力 \( F_c = \frac{m v^2}{r} \) が重力 \( F_g = \frac{G M m}{r^2} \) を補償することになります。ここで、 \( G \) は重力定数、 \( M \) は星の質量、 \( r \) 軌道半径。

方程式の導出

\( F_c \) と \( F_g \) を等しくすると、次のようになります。

\( \frac{m v^2}{r} = \frac{G M m}{r^2} \)

惑星の質量 \( m \) が消去されると、公転速度が惑星の質量に依存しないことがわかります。

\( v = \sqrt{\frac{G M}{r}} \)

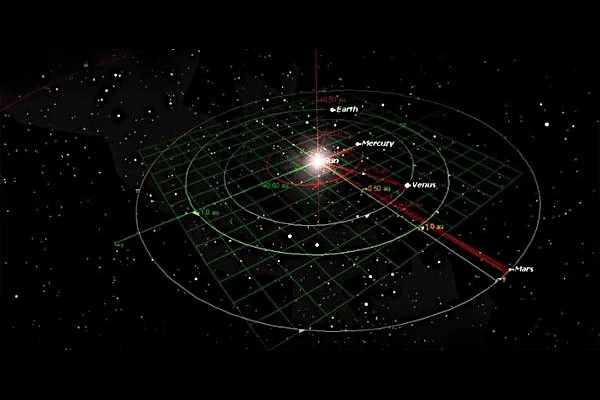
この基本的な関係は、星からの距離の関数としての公転速度の依存性を表します。太陽に近い惑星 (水星など) は公転速度が速く、遠い惑星 (海王星など) はゆっくりと動きます。

物理的解釈

この方程式は、次の経験則を示しています。ヨハネス・ケプラー(1571-1630) と重力理論アイザック・ニュートン（1643-1727）。公転速度は、法則 \( v \propto r^{-1/2} \) に従い、距離の平方根に応じて減少します。これは、ケプラーの第 3 法則によって回転周期 \( T \) を条件付けします。 \( T^2 \propto r^3 \)。

したがって、太陽系の各惑星の平均公転速度は、太陽質量 \( M_\odot = 1.989 \times 10^{30}\, \mathrm{kg} \) とメートルで表される平均公転半径から計算できます。

太陽系の惑星の平均公転速度
惑星	太陽からの平均距離 (10⁶キロ）	軌道速度 (km/s)	恒星周期 (日)
水銀	57.9	47.9	87.97
金星	108.2	35.0	224.70
地球	149.6	29.8	365.26
行進	227.9	24.1	686.98
木星	778.6	13.1	4332.6
土星	1433.5	9.7	10759
天王星	2872.5	6.8	30688
ネプチューン	4495.1	5.4	60182

ソース：ジェット推進研究室 – 太陽系ダイナミクス。

アプリケーションと制限事項

方程式 \( v = \sqrt{\frac{G M}{r}} \) は完全な円軌道を仮定し、惑星間の重力擾乱を無視しています。実際には、軌道は楕円形です。速度は位置に応じて変化し、位置に応じて大きくなります。近日点そしてより弱いアフェリア。このバリエーションはケプラーの面積の法則に従います。つまり、光線ベクトルは同じ時間で等しい面積を掃引します。

桁違いの規模とエネルギーの重要性

円軌道上の惑星の総軌道エネルギー (運動 + ポテンシャル) は次のとおりです。

\( E = -\frac{G M m}{2 r} \)

負の値は、惑星がその星と重力で結びついていることを示します。惑星を解放するには、つまり、惑星に到達するには、エネルギー \( \geq |E| \) を提供する必要があります。リリーススピード\( v_e = \sqrt{\frac{2 G M}{r}} \)、または \(\sqrt{2}\) 倍の軌道速度。