最終更新日: 2023 年 5 月 4 日

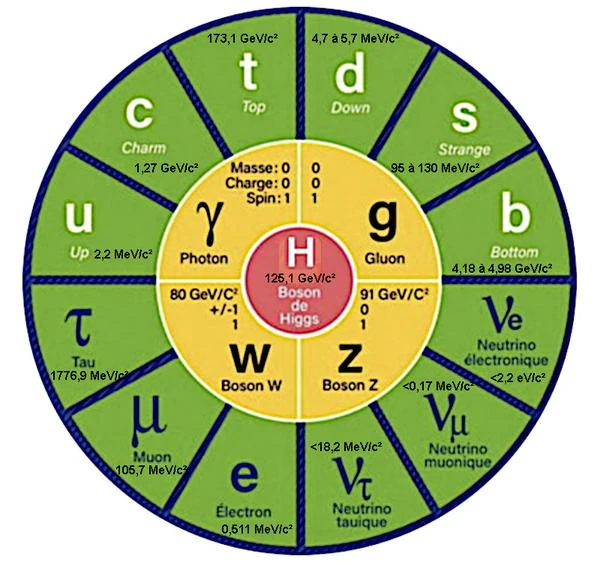
なぜ素粒子には質量がないのでしょうか?

E=mc² のおかげで、素粒子は質量を持たなくなります。

素粒子とその相互作用の世界は、いわゆる素粒子物理学の標準モデルによって記述されます。
標準模型では、光子やグルーオンなどの一部の素粒子は質量のない粒子とみなされます。しかし、クォーク、W ボソン、Z ボソン、レプトンなどの他の粒子の場合は、実験的に質量を測定します。質量はエネルギーに変換でき、またその逆も可能であり、結果を比較しやすくするために電子ボルトで測定されます。
ただし、標準モデルは、固有質量を持たない素粒子、つまり、その性質に固有の質量を持たない素粒子にのみ適用されます。さらに、これらの粒子は光の速度で移動する必要があります。
この美しい物理学の構造は、2012 年のヒッグス粒子の発見により、この行き詰まりから抜け出すことができました。
実際、粒子の質量はもはや固有の特性ではなく、ヒッグス場との相互作用から生じます。ヒッグス場との相互作用が強いほど慣性が大きくなり、いわゆる質量が生じます。

アルバート・アインシュタイン (1879-1955) の特殊相対性理論は、エネルギーと質量は同等であり、方程式 E=mc によって関係付けられると述べています。²。
つまり、巨大な物体には質量があるという理由だけでエネルギーがあり、このエネルギーは巨大であり、物質 1 グラム = 8.99 x 10¹² ジュール (J) です。
粒子に関しては、このエネルギーは静止している粒子の質量を表します。ただし、粒子が動いている場合、この方程式は運動エネルギーを考慮する必要があります。
E=mc² は 1912 年にのみ登場しました。 1905 年に、総エネルギーは次のように公式化されました E² = m²c⁴ + p²c²。運動量 (p) がゼロの場合、2 つの方程式は同一です。この方程式は次のように表すこともできます: E = √(m²c⁴ + p²c²)
この方程式 E² = (pc)² + (mc²)²、または同等の E = √(m²c⁴ + p²c²) では、粒子の質量エネルギーと運動エネルギーが考慮されます。
まさにこの公式によって、質量ゼロの粒子の存在が可能になります。実際、その運動量がゼロでない場合、粒子は質量を持たず、エネルギーを持つことができます。この場合、質量のない粒子は静止していることができず、必然的に光の速度を持ちます。

なぜ質量のない粒子が光速で移動しなければならないのでしょうか?

物体が静止している場合、その総エネルギーは E=mc² です。この場合、物体の慣性 (慣性質量) をその総質量として測定します。つまり、慣性質量 = E/c² となります。
物体が動いている場合、その総エネルギーは E = √(m²c⁴ + p²c²)、つまり E = mc² + pc (運動エネルギー) です。
したがって、質量のない粒子の場合、E² = (mc²)² + (pc)² または E = mc² + pc または E = pc
方程式 E = mc² + pc において、pc は粒子の運動エネルギーを表します。 p は粒子の運動量で、質量 m に速度 v を掛けたものに等しく、c は光の速度です。したがって、pc = mvc となります。ここで、m は粒子の質量、v は粒子の速度です。
質量のない粒子 E = c の場合、これが、質量のない粒子が 1 つの速度、つまり光の速度しか持ち得ない理由です。

なぜ光の速度が制限速度になるのでしょうか?

慣性とは、静止した物体を動かしたり、移動中に速度を変化させたりするために必要なエネルギーです。実際、物体が大きければ大きいほど、動きの変化に強く抵抗します。言い換えれば、物体の質量が大きくなるほど、速度とともに慣性が増大するため、加速または減速することがより困難になります。慣性が非常に大きくなり、限界速度、つまり光の速度に達する瞬間が来ます。