最終更新日: 2024 年 6 月 11 日

質量のない光子がなぜエネルギーを持つのでしょうか?

画像の説明: 光子は正弦波で表され、電磁波としての性質を象徴しています。光子のエネルギーはその周波数 (E=hν) に比例します。赤い点はフォトンの粒子の側面を表しています。正弦波上の光子には運動量 (p = E/c = hν/c) があります。

質量とエネルギーの関係

方程式 E=mc²アルバート・アインシュタイン (1879-1955) によって提案されたものでは、物体の質量 m とエネルギー E の関係が確立され、c は真空中の光の速度を表します。
この方程式は、質量がエネルギーに変換され、またその逆も可能であることを意味します。方程式 E=mc² によれば、質量のない粒子 (m=0) がエネルギー (E ≠ 0) を持つことができるということは逆説的に見えるかもしれません。
質量 m=0 の光子は、方程式 E=mc によりエネルギー E≠0 になります。²特に静止している粒子に適用されます。実際、粒子のエネルギーと質量の関係は、特殊相対性理論の完全な方程式によって与えられます。²=(パソコン)²+(m₀c²)²ここで、p は力積、m は₀は残りの質量です。

光子の休息は不可能

光子は質量も電荷も持たない粒子です。それは電磁場の量子であり、この場の基本的な励起であることを意味します。その記述はマクスウェル方程式によって支配され、量子レベルでは質量のない粒子のディラック方程式によって支配されます。
したがって、光子は、その周波数と波長によって特徴付けられる、量子エネルギーのキャリアとしての本質的な性質によって定義されます。 m であることを考えると、₀=0 の光子が静止している (v=0) 場合、これはそのエネルギー E がゼロになることを意味します (p=0 から v=0 であるため)。しかし、光子の存在は、そのエネルギーの所有と切り離すことができません。エネルギーがゼロの光子は物理的な意味を持たず、存在できません。
アインシュタインの理論は、質量を持つ粒子が到達または超えることのできない普遍的な限界速度 c が存在すると予測しています。この速度は真空中の光の速度に相当します。したがって、光子が存在するには、常に速度 c で移動している必要があります。

エネルギーと光子

したがって、光子は静止質量 (m₀=0) 常に光の速度で移動します。 c. それらには運動量 (p) があり、したがってエネルギーがあります。
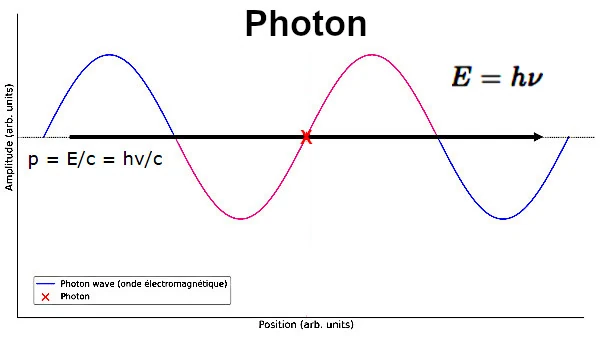
光子のエネルギーと運動量の関係は、方程式 E=pc で与えられます。
光子のエネルギーはプランクの方程式 E=hν で与えられます。ここで、E はエネルギー、h はプランク定数 (6.626×10^−34J、ν (ν) は光子の周波数です)。
この関係 E=hν は、光子のエネルギーがその周波数に比例することを示しています。

関係 E=pc とプランク方程式を組み合わせると、p = E/c = hν/c が得られます。

相対論的な文脈では、運動中の大質量粒子の場合、総エネルギー E は相対論的方程式 E で与えられます。²=(m₀c²)²+ (パソコン)²。
光子の場合、静止質量 m はゼロであるため、この方程式は E=pc に単純化されます。

結論

要約すると、光子には静止質量はありませんが、エネルギーと運動量はあります。光子のエネルギーは方程式 E=hν によってその周波数に関連付けられ、その運動量は p=E/c によって与えられます。方程式 E=mc²静止している粒子には適用されますが、フォトンには静止は存在しません。光子は電磁場の基本励起です。