アイザック・ニュートン(1643-1727)の三法則は、古典力学の概念的・数学的基礎を成します。 これらの法則は、力、質量、加速度の間の基本的な関係を方程式で表現しています。 これらの法則は、1687年の『自然哲学の数学的諸原理』で発表され、地上および天体の物体の運動を驚くべき精度で理解し予測することを可能にしました。
第一法則は慣性の法則と呼ばれ、物体は外力が作用しない限り、静止または等速直線運動を続けると主張します。 これは方程式で \(\sum \vec{F} = 0 \Rightarrow \vec{v} = \text{一定}\) と表されます。 この法則は、物体が正味の加速度を受けない慣性基準系の存在を示しています。
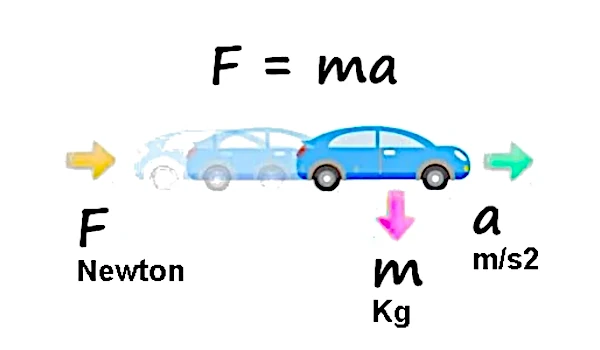
第二法則は、加えられた力と速度の変化を定量的に関連付けます。 これは \(\sum \vec{F} = m \vec{a}\) と書かれ、\(m\) は物体の質量、\(\vec{a}\) は加速度です。 この方程式はニュートン力学の中核を表しており、運動の変化は力によって引き起こされ、その比例は質量に依存します。 非慣性基準系では、この関係を回復するために見かけの力を導入する必要があります。
第三法則は、物体Aが物体Bに及ぼす作用には、BがAに及ぼす大きさが等しく反対向きの反作用が存在すると述べています。 数学的には \(\vec{F}_{AB} = -\vec{F}_{BA}\) と表されます。 この作用・反作用の原理は、相互作用の対称性と孤立系における運動量の保存を表しています。 例えば、大砲が砲弾を発射するとき、砲弾を加速する力は同時に大砲の反動を引き起こします。
これら三つの法則は、人間や惑星のスケールでの落下、振動、軌道、衝突など、あらゆる力学的状況を記述することを可能にします。 これらは力と運動の間の明確な因果関係を導入し、質量を力学的エネルギーと相互作用を結びつける普遍的な定数とします。 この枠組みは、アルバート・アインシュタイン(1879-1955)が1905年に定式化した特殊相対性理論の登場まで物理学を支配しました。特殊相対性理論は、ニュートンの法則が光速に比べて非常に遅い速度 \(v \ll c\) でのみ近似的に成り立つことを示しています。
N.B.:
ニュートンの法則は、相対論的速度や素粒子のスケールでは正確でなくなります。 それらは相対性理論と量子力学の法則に置き換えられます。 しかし、実用的な場合の99.9%では完全に有効であり、すべての工学分野で使用されています。
| 法則 | 数学的定式化 | 物理的原理 | コメント |
|---|---|---|---|
| 第一法則:慣性 | \(\sum \vec{F} = 0 \Rightarrow \vec{v} = \text{一定}\) | 力なき運動の保存 | 慣性基準系を定義 |
| 第二法則:運動 | \(\sum \vec{F} = m \vec{a}\) | 加速度に比例する力 | 力学計算と軌道の基礎 |
| 第三法則:作用・反作用 | \(\vec{F}_{AB} = -\vec{F}_{BA}\) | 力学的相互作用の対称性 | 運動量の保存 |
出典:Stanford Encyclopedia of Philosophy – Laws of Motion と Physics.info – Newton’s Laws。