最終更新日: 2024 年 11 月 6 日

ネーターの定理

画像の説明: の肖像画アマリー・エミー・ネーター(1882-1935)、ドイツの数学者。ネーターの定理は、物理法則は対称であり、この対称性が保存則につながると述べています。画像の出典：パブリックドメイン。

ネーターの定理の定義

ネーターの定理の宣言: 「作用積分を不変のままにするあらゆる無限小変換は、保存される量に対応します。」

ザネーターの定理1915 年に実証され、1918 年に出版された理論物理学の基本的な概念であり、保存法そして対称性物理的なシステム。
言い換えれば、「物理法則が、たとえ小さな変化（空間の運動や時間の変化など）の後でも同じままであるならば、時間の経過とともに変化しない量、つまり保存される量（エネルギー、運動、電荷など）が存在する。」ということです。

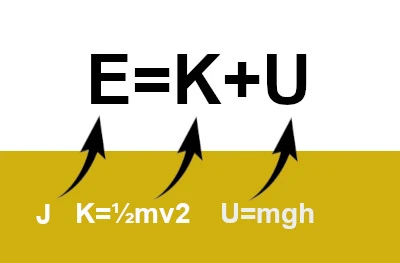
振り子の例: 単振り子の全機械エネルギー E は、その運動エネルギー (K) とその位置エネルギー (U) の合計として表すことができます。E=K+U。

L'運動エネルギー振り子の K は次の式で与えられます: K=1/2mv²ここで、m は振り子の質量、v は振り子の速度です。

L'位置エネルギー重力による U は次の式で与えられます。 U=mgh ここで、m は振り子の質量、g は重力による加速度、h は平衡位置に対する振り子の高さです。

L'総機械エネルギー振り子の E は一定のままです。これは、運動エネルギーは振り子の速度に応じて変化する可能性がありますが、E を一定に保つための位置エネルギーの対応する変化によって補償されることを意味します。

これは、ネーターの定理と一致して、システムの総力学的エネルギーの保存を反映しています。

注： :
そこには保管数量時間の経過とともに一定に保たれる物理量です。たとえば、エネルギー、運動量 (運動量)、または角運動量は保存量です。

物理学における対称性の概念

対称性は単に美しいだけではありません。それらは、物理学の多くの基本原理の基礎を構成します。ネーターの定理のおかげで、各対称性は、エネルギー保存、電荷保存、運動量、角運動量などの保存則に関連付けられていることがわかります。

対称性は、自然法則における不変性または不変条件を表します。物理学ではさまざまなタイプの対称性があり、それぞれのタイプには特定の意味があります。

平行移動対称性

そこには並進対称性これは、システムが回転せずに空間を移動するときに物理法則が変化しないことを意味します。これは、実験の結果が空間内の物体の絶対位置に依存しないことを意味します。パリでも、ニューヨークでも、地球でも、火星でも、宇宙のどこでも結果は同じだろう。系を数キロメートルまたは数光年動かしても物理法則が変わらない場合、系の運動量ベクトルは保存されます。したがって、並進対称性は次のことを意味します。運動量の保存。

回転対称性

そこには回転対称物理法則は固定軸の周りの回転下では不変であると述べています。言い換えれば、ある点を中心にシステムを回転させても、その動作を支配する法則は同一のままです。たとえば、惑星が太陽の周りを周回するとき、軌道を変える外力が作用しなければ、その角運動量は一定のままです。したがって、回転対称の結果、角運動量の保存。

時間的対称性

そこには時間的対称性これは、物理法則が時間の経過とともに変化しないことを意味します。これは、法則は過去も現在も同じであり、数百万年後も同じであることを意味します。たとえば、摩擦やその他の散逸力が存在しない場合、振り子の機械的エネルギー (運動エネルギーと位置エネルギーの合計) は動作中一定のままです。運動エネルギー（振り子が最低点にあるとき）と位置エネルギー（振り子が最高点にあるとき）は相互に変換されますが、総和は変わりません。したがって、振り子の時間的対称性は、省エネ。閉鎖系では、総エネルギーは時間が経っても一定のままです。

パリティ対称性

そこにはパリティ対称性空間反転中の物理法則の不変性、つまり、点のすべての座標が中心に対して反転する場合: (��,��,��)→(−��,−��,−��)に関するものです。たとえば、電子が陽子でできたターゲットに向けられると、電子は電磁相互作用を介して陽子と相互作用します。電子と陽子の座標を考慮すると、パリティ変換は粒子の位置を逆転することで構成されます。特定の方向に移動する電子の場合、その空間座標の符号を変更しても、弾性拡散を支配する法則はこの変換下では変化しません。したがって、パリティ対称性の結果、総エネルギーの節約そして総運動量。

電荷対称性

そこには電荷対称性すべての電荷が逆転しても物理法則は変わらないと述べています。たとえば、電子を陽電子に、または陽子を反陽子に置き換えた場合、相互作用の結果は変わらず、消滅プロセスも同じままです。したがって、電子陽電子消滅は、電荷保存。

ゲージの対称性

ザゲージ対称性粒子に関連付けられた場の変換であり、物理法則は変わりません。電磁気学の理論、弱い相互作用と強い相互作用はすべてゲージ理論です。たとえば、場に関連付けられたポテンシャルを変更した場合、ゲージの対称性によって運動方程式が維持され、物理的な観測値 (電場や磁場など) は変化しません。したがって、ゲージの対称性は、電荷保存(量子電気力学において)、または色電荷保持（量子色力学において）。