最終更新日: 2023 年 4 月 20 日

エネルギー保存: 物理学の基本原理

画像の説明: エネルギー保存は物理学の基本原理です。環境と相互作用しない孤立したシステムの総エネルギーは、時間が経っても一定のままです。それは作成したり破壊したりすることはできませんが、ある形式のエネルギーから別の形式のエネルギーに変換することはできます。
しかし、摩擦力を受けない真空中の振り子は、理論的には永久運動をする可能性があります。しかし、たとえ宇宙であっても、動いている振り子はエネルギーを失い続けます（振り子自体の内部摩擦、他のシステムへのエネルギーの伝達、温度の影響など）。このエネルギーの損失により、最終的には振り子が停止します。したがって、これらのエネルギー損失を補う外部エネルギー源がなければ、物体を永久運動させることは不可能です。

運動エネルギー

運動エネルギーは物理学の基本的な特性です。これは、速度による物体の動きに関連するエネルギーの一種です。運動エネルギーはスカラー量です。つまり、大きさはありますが方向はなく、数値によってのみ定義される量です。
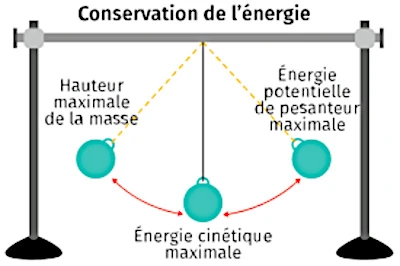
振り子が動いているとき、振り子はその運動エネルギー (その動きに関連する) とその位置エネルギー (その位置に関連する) の間でエネルギーを継続的に交換します。振り子がスイングするたびに、システムの総エネルギー (運動エネルギーと位置エネルギーの合計) は一定のままですが、エネルギーは 2 つの形態の間で継続的に伝達されます。
物体の「生きる力」という名前で導入された運動エネルギーの概念は、ライプニッツ (1646-1716) とエミリーデュシャトレ (1706-1749) によって発見されました。
方程式は次のとおりです。
E_c = 1/2 mv^2、ここで E_c は運動エネルギー、m は物体の質量 (kg)、v は速度 (m/s) を表します。
したがって、運動エネルギーは物体の質量の 1/2 と速度の 2 乗に直接依存します。一般に、より速い車両やより重い車両がその動きを維持するためにより多くのエネルギーを必要とするのはこのためです。

位置エネルギー

位置エネルギーは、重力場の位置に関連付けられたエネルギーの形式です。物体が高くなるほど、その物体が持つ位置エネルギーは大きくなります。このエネルギーは水力発電ダムで毎日利用されています。
方程式は次のとおりです。
E_p = mgh
したがって、位置エネルギーは、物体の質量 m (kg)、重力 g (9.81 m/s2)、および基準レベルに対する物体の位置の高さ h (m) に直接依存します。
位置エネルギーは、適切な物理プロセスを通じて、運動エネルギー (運動に関連する) や熱エネルギー (熱に関連する) など、他の形式のエネルギーに変換できます。たとえば、自由落下する物体は、地面に向かって加速するときに、その重力位置エネルギーを運動エネルギーに変換します。
mgh = 1/2mv^2
v^2 = 2gh (質量は消滅するため、真空中での物体の落下には重要ではありません)
h = 1/2g v^2
注: ポテンシャルエネルギーは相対量であり、特定の基準位置の選択に依存します。計算では 2 つの位置間のポテンシャルエネルギーの差のみが重要です。