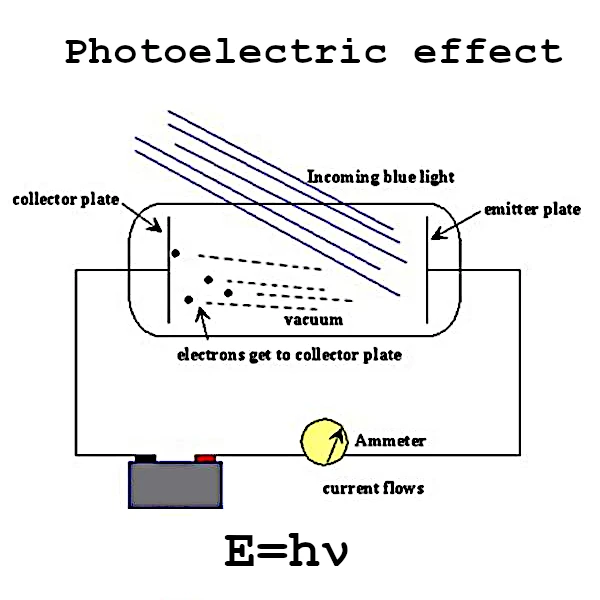
光電効果は、現代物理学の最も基本的な発見の一つです。この現象は19世紀末に初めて観測され、光と物質に対する理解を根本から変えました。
光電効果の理解は、量子力学の発展において決定的な転機となりました。光の量子仮説を検証し、物理学の新時代を切り開きました。
20世紀初頭、物理学者たちは、古典光学の基礎を揺るがす不可解なパラドックスに直面していました。ジェームズ・クラーク・マクスウェル（1831-1879）によって確立された波動説によれば、光波が運ぶエネルギーはその強度に比例するとされていました。
物理学者たちは、次のように予想していました：
しかし、フィリップ・レーナルト（1862-1947）らの綿密な実験は、全く予想外の振る舞いを明らかにしました：
このパラドックスは、赤色光で特に顕著でした：どれだけ強くても、亜鉛のような金属から電子を一つも放出できませんでした。一方、非常に弱い紫色光でも、電子は即座に放出されました。
古典理論と実験観測の間のこの根本的な矛盾は、新しい光の概念によってのみ解決できる理論的な行き詰まりを生み出しました。
1905年、アルバート・アインシュタイン（1879-1955）は、1921年のノーベル賞をもたらす革命的な説明を提案しました。彼は、光が光子から成り、それぞれが明確なエネルギーを持つと主張しました： \( E = h \nu \) ここで、\( h \) はプランク定数、\( \nu \) は光の周波数です。
注：
プランク定数は非常に小さい値です (\( h = 6.62607015 \times 10^{-34} \mathrm{J \cdot s} \))。このため、量子効果はマクロスケールでは観測できませんが、原子や素粒子のスケールでは支配的になります。
光電効果は、次の3つの基本法則に従います：
放出される電子の最大エネルギーは次の式で表されます： \( E_{max} = h\nu - \phi \) ここで、\( \phi \) は物質の仕事関数を表します。
注：
光電効果は、光の量子的な性質を確立する上で決定的でした。古典的な波とは異なり、エネルギーは離散的なパケット（光子）として交換され、そのエネルギーは周波数のみに依存します。
| 現象 | 光の性質 | 電子のエネルギー | 効果の閾値 |
|---|---|---|---|
| 光電効果 | 粒子（光子） | 周波数に依存 | 最小周波数が必要 |
| 古典的熱効果 | 波動 | 強度に依存 | 閾値なし |
出典：1921年ノーベル物理学賞 - アルバート・アインシュタインおよびブリタニカ百科事典 - 光電効果。
アルバート・アインシュタイン（1879-1955）によって解読された量子現象である光電効果は、現代社会に不可欠な多くの技術の基本原理となっています。
太陽電池は最もよく知られた応用例です。太陽光の光子が半導体（通常はシリコン）に当たると電子を放出し、直流電流を生成します。
CCDおよびCMOSセンサーは、すべての現代のカメラに搭載されています。各ピクセルには、受け取った光の強度に比例して電子を生成するフォトダイオードが含まれています。
検出システムは、フォトディテクターのさまざまな種類の放射線に対する精密な感度を利用しています（セキュリティゲート、煙検知器、テレメーターなど）。
科学研究では、物質分析や宇宙探査（光電子増倍管、分光計、宇宙望遠鏡など）に極めて敏感な光電検出器を使用しています。
医療分野でも、光電効果の応用が診断と治療（内視鏡カメラ、陽電子放出断層撮影、血液分析用フォトディテクターなど）に利用されています。
経済的影響：光電効果に基づく技術の市場は、年間数千億ユーロに達し、特に太陽光発電とデジタルイメージング分野で急速に成長しています。
光速：宇宙の絶対的な限界を超えられない理由 
現実は我々の手の届かないところに：証明できない真実 
50の方程式で解き明かす宇宙の物理：取扱説明書 
カヤ方程式：脱炭素化を複雑にする方程式 
宇宙における超えられない速度：エネルギーが無限になるとき 
電磁的暴走：光速の秘密 
光電効果を理解する：光と電子 
地平線はどれくらいの距離にあるのか？ 
太陽光パネルはどのように電気を電力網に送り込むのか？ 
運動量の力学：ロケットやクラゲの推進を説明する 
電子のエネルギーが化学的性質を決定する仕組み 
量子不確定性の重要な役割：どの粒子も静止することはできない 
エネルギーとパワー：混同しないで、時間がすべての違いを生む 
なぜ寒さには限界があるのに暑さにはないのか？ 
ガリレオの落体の法則 
理想気体の法則：一つの方程式、無数の応用 
シュレーディンガー方程式は物質の見方を革命的に変えました 
ネーターの定理の魔法：最小作用の原理から保存則へ 
重力質量と慣性質量の等価性と等価原理
物理学の第三方程式：衝突を理解するための運動量 
物理学の第二の基本方程式：保存される量の直感 
物理学の第一方程式：力を数学的に表現する方法 
電磁力またはローレンツ力 
受け取る太陽エネルギーは傾斜角によって変化する 
なぜ大理石は木よりも冷たいのか？ 
なぜ質量のない光子がエネルギーを持つのか？ 
ベイズの定理と人工知能 
物理学の7つの基本定数 
星間空間で感じる温度はどれくらいか？ 
黒体放射の曲線：プランクの法則 
等価原理：重力効果は加速度と区別がつかない 
E=mc²：宇宙の4つの基本概念を再考する 
太陽の重さを測る方法 
自由落下の方程式（1604年） 
クーロン vs ニュートン：宇宙の力の神秘的な類似性 
エントロピーに関するボルツマンの方程式（1877年） 
特殊相対性理論の方程式（1905年） 
一般相対性理論の方程式（1915年） 
惑星の自転方程式：角運動量と重力平衡の間 
惑星の公転速度の方程式 
プランクの方程式 
数学なしでシュレディンガー方程式を理解する 
ニュートンの三法則：落ちるリンゴから惑星の軌道まで 
マクスウェルの方程式 
ディラックの方程式 
エネルギー保存則 
電磁誘導の方程式 
なぜ素粒子は質量を持たないのか？ 
熱と温度の違い