最終更新日: 2024 年 6 月 25 日

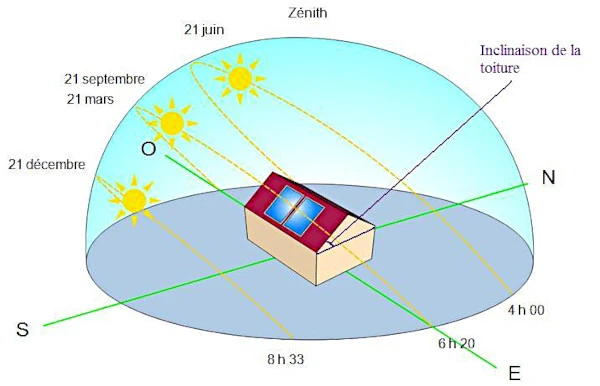
傾きによって受け取る太陽エネルギーは変わる

受け取る太陽エネルギーに対する太陽の角度の影響

ランベルトの法則 (Johann Heinrich Lambert 1728-1777) は、表面への入射太陽エネルギー I の強度は、太陽光線と表面の法線との間の入射角 θ の余弦に比例すると述べています: I = I₀ cos(θ)
私₀は、表面に垂直なときの太陽エネルギーの強度、つまり、平方メートルあたりのワット数 (W/m²) で表した光の強度です。
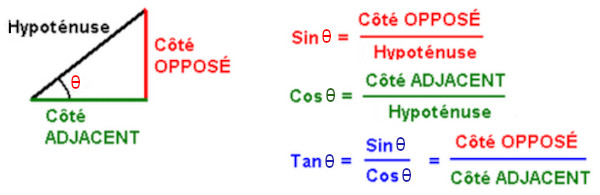
直角三角形の角度の余弦は、斜辺の長さに対する角度に隣接する辺の長さの比です。
θ は地球の表面に対する入射角です。入射角は、問題の表面に対する太陽の相対位置によって決まります。一般に、この角度は緯度、曜日、時刻によって異なります。水平面の場合、入射角は太陽高度角（太陽高度）と太陽方位にも影響されます。

受け取る太陽エネルギーの計算

平らな傾斜面の場合、受け取る太陽エネルギーは、表面全体の太陽エネルギーの強度を積分することによって計算できます。 E が単位面積あたりに受け取られるジュール (J) 単位のエネルギーの場合: E = E₀ cos(θ) (E₀光線が垂直な場合に単位面積あたりに受け取るエネルギーです)。

エネルギー E と強度 I の関係は、表面が受け取る総エネルギーが光の強度、表面積、露光時間に比例することを示しています。
I = E/A.t
I は、1 平方メートルあたりのワット数 (W/m²) で表した光の強度です。
E はジュール (J) 単位のエネルギーです。
A は平方メートル (m²) 単位の面積です。
t は秒単位の時間です。

例

入射角 (垂直に対して) θ = 30 度の場合、表面が受け取る太陽エネルギーはいくらですか?
表面に垂直な太陽エネルギーの強度、I0 = ≈ 1000 W/m²、太陽定数とも呼ばれます (これは太陽正午の晴天の典型的な値です)。
私＝私₀ cos(θ)
cos(30°) = √²/2 ≈ 0.866
I = 1000 W/m² x 0.866 ≈ 866 W/m²、または太陽定数の 86%。

入射角 θ = 45 度の場合、表面が受け取る太陽エネルギーはいくらですか?
私＝私₀ cos(θ)
cos(45°) = √²/2 ≈ 0.707
I = 1000 W/m² x 0.707 ≈ 707 W/m²、または太陽定数の 70%。

入射角 θ = 90 度の場合、表面が受け取る太陽エネルギーはいくらですか?
私 = 私₀ cos(θ)
cos(90°) = 0
I = 1000 W/m² x 0 ≈ 0 W/m²。

• 30 度の場合、表面は約 866 W/m² を受け取ります。
• 45 度の場合、表面は約 707 W/m² を受け取ります。
• 66 度では、表面は約 406 W/m² を受け取ります。
• 90 度では、表面は 0 W/m² を受け取ります。