最終更新日: 2025年12月5日

電磁的暴走：光速の秘密

マクスウェルの4つの方程式

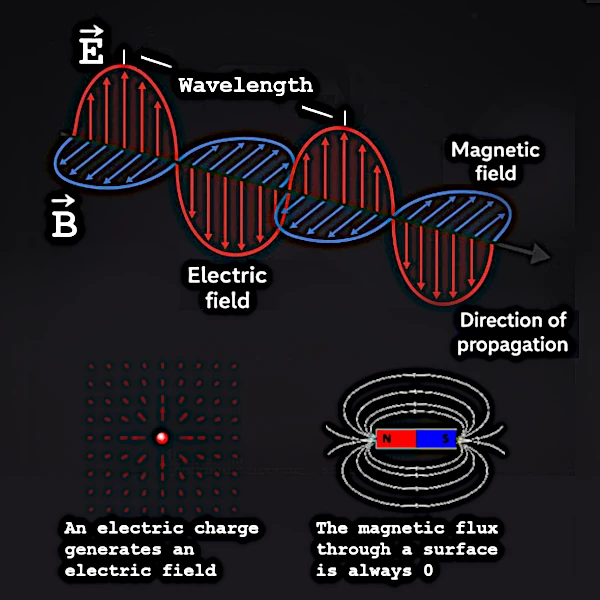
すべての電磁現象は、4つの基本的な関係式、すなわちマクスウェルの方程式に還元されます。これらの方程式だけで、電場と磁場のダイナミクスに関するすべてが予測されます。

電気に関するガウスの法則: \(\nabla \cdot \mathbf{E} = \dfrac{\rho}{\varepsilon_0}\) (電場の発散は電荷密度 \(\rho\) に比例 → 電荷は周囲に電場を作り出す)
磁気に関するガウスの法則: \(\nabla \cdot \mathbf{B} = 0\) (閉曲面を通る磁束の総和はゼロ → 磁力線は閉ループを形成し、磁気単極子は存在しない)
ファラデーの法則: \(\nabla \times \mathbf{E} = -\frac{\partial \mathbf{B}}{\partial t}\) (時間変化する磁場は回転電場を生じる)
アンペール・マクスウェルの法則: \(\nabla \times \mathbf{B} = \mu_0 \varepsilon_0 \frac{\partial \mathbf{E}}{\partial t}\) (時間変化する電場は磁場を生じる)

最後の2つの方程式が暴走の謎の鍵です。時間変化する磁場 (\( \partial \mathbf{B}/\partial t \)) は回転電場を生じ、対称的に、時間変化する電場 (\( \partial \mathbf{E}/\partial t \)) は回転磁場を生じます。この動的結合が伝播中に自己持続します。

マクスウェルと光速の発見

ジェームズ・クラーク・マクスウェル（1831–1879）が19世紀に電気と磁気の法則を統一したとき、彼は驚くべき現象を発見しました：電場または磁場の局所的な撹乱は、真空中で自ら伝播する波を生み出し、追加のエネルギーを必要としません。

波動方程式と光速の予測

マクスウェルは、この波が真空の2つの性質によって決まる有限の速度で移動することを示しました：

その速度は \( c = \frac{1}{\sqrt{\mu_0 \varepsilon_0}} \) で与えられます。

μ₀: 真空の磁場を運ぶ能力
ε₀: 真空の電場を通す能力

光は電磁波である

ファラデーの法則とアンペール・マクスウェルの法則を組み合わせることで、彼は波動方程式を得ました。μ₀とε₀の値を代入すると、 \( c \approx 300,000 \) km/s、すなわち光速が得られました！

マクスウェルの結論

1865年、マクスウェルは光は電磁波であると結論づけました。これはラジオ波やマイクロ波と同じです。この発見は物理学に革命をもたらしました。

N.B.:
マクスウェルの時代（1865年）、光速はまだ高精度で知られていませんでした。当時利用可能な実験的測定、特にアルマン・フィゾー（1819-1896）とアルバート・マイケルソン（1852-1931）によるものでは、\( v \) をかなりの誤差範囲で推定することができました。マクスウェルの理論的計算は、後に確認される値に非常に近い値を与え、これは彼の理論に対する印象的な検証となりました。

E場とB場の伝播速度の計算

マクスウェルが電気と磁気の法則を組み合わせたとき、彼は局所的に電場または磁場が撹乱されると自己持続する構造を発見しました。この「暴走」は安定しており、増幅せず、内部エネルギー源も持ちません。真空は波を運ぶだけで、エネルギーを供給しません。

波動方程式と光速の予測

この \( \mathbf{B} \) と \( \mathbf{E} \) の間の動的ループは、真空中を有限の速度で伝播する構造を生み出します。

4番目の方程式の項 \(\mu_0 \varepsilon_0\) が光速を決定します： \( c = \frac{1}{\sqrt{\mu_0 \varepsilon_0}}. \)

\( \mu_0 \): 真空の透磁率定数、または真空の磁場を運ぶ能力
\( \varepsilon_0 \): 真空の誘電率定数、または真空の電場を通す能力

電磁波動方程式の導出

ファラデーの法則とアンペール・マクスウェルの法則を数学的に組み合わせる（一方の回転を取り、もう一方を使用する）ことで、結合を排除し、各場を個別に記述する方程式を得ます。

電場の波動方程式

電場については、次のようになります： \( \nabla^2 \mathbf{E} = \mu_0 \varepsilon_0 \frac{\partial^2 \mathbf{E}}{\partial t^2} \) これは波動方程式の古典的な形式です。項 \( \mu_0 \varepsilon_0 \) は時間の二階微分の前にあります。数理物理学では、標準的な波動方程式は \( \nabla^2 \psi = \frac{1}{v^2} \frac{\partial^2 \psi}{\partial t^2} \) と書かれ、\( v \) は伝播速度です。

波の速度との同定

直接の同定により： \( \frac{1}{v^2} = \mu_0 \varepsilon_0 \quad \Rightarrow \quad v = \frac{1}{\sqrt{\mu_0 \varepsilon_0}} \)

計算結果：光は電磁波である

マクスウェルは、当時知られていた定数を用いてこの値を計算しました：

\( \mu_0 = 4\pi \times 10^{-7} \, \text{N} \cdot \text{A}^{-2} \)
\( \varepsilon_0 \approx 8.854 \times 10^{-12} \, \text{C}^{2} \cdot \text{N}^{-1} \cdot \text{m}^{-2} \)

結果は驚くべきものでした：\( v \approx 2.998 \times 10^{8} \, \text{m/s} \)、波の速度は実験的に測定された光速に一致しました！

N.B.:
この数学的証明は真空、すなわち電荷や電流のない状態（\( \rho = 0, \, \mathbf{J} = 0 \)）を仮定しています。推論は、ファラデーの法則の回転を取り、ベクトル恒等式 \( \nabla \times (\nabla \times \mathbf{E}) = \nabla(\nabla \cdot \mathbf{E}) - \nabla^2 \mathbf{E} \) を使用し、ガウスの法則（真空中では \( \nabla \cdot \mathbf{E} = 0 \)）とアンペール・マクスウェルの法則を組み合わせることで行われます。これにより、磁場 \( \mathbf{B} \) に対しても同じ波動方程式が得られます。この理論的予測は、ジェームズ・クラーク・マクスウェル（1831-1879）による1865年のもので、ハインリヒ・ヘルツ（1857-1894）が1887年に最初の無線波を生成したことで実験的に確認されました。

マクスウェル方程式の限界

マクスウェルは、電磁波が真空中を一定の速度で伝播することを発見しましたが、これが限界速度であるという証明はまだありませんでした。マクスウェルはまだ相対性理論を知りませんでした。したがって、これが普遍的な限界速度であるとは考えられませんでした。普遍的な限界の概念は、マクスウェルのずっと後に現れた特殊相対性理論とともに現れました。

アルバート・アインシュタイン（1879-1955）の特殊相対性理論（1905年）によって初めて、真空中の光速 \( c \) は、情報、エネルギー、またはあらゆる物理的相互作用が伝播できる最大速度として認識されました。つまり、\( c \) は時空の構造によって課せられた基本的な限界であり、マクスウェルの方程式の単なる結果ではありません。

結論：覚えておくべきこと

電磁現象はマクスウェルの方程式に従い、次のように要約できます：

電荷はその周りに電場を作り出します。
時間変化する磁場は電場を生じます。
時間変化する電場は、今度は磁場を作り出します。
この2つの場は自己持続し、空間を光速で伝播する電磁波として現れます。

したがって、光およびすべての電磁波は、真空中での電場と磁場の自己持続現象の表れに過ぎません。

同じテーマの記事

電磁的暴走：光速の秘密

光電効果を理解する：光と電子

地平線はどれくらいの距離にあるのか？

太陽光パネルはどのように電気を電力網に送り込むのか？

運動量の力学：ロケットやクラゲの推進を説明する

原子内の電子のエネルギー分布

ハイゼンベルクの不確定性原理：量子的不確定性を理解する

エネルギー、パワー、時間の関係

なぜ寒さには限界があるのに暑さにはないのか？

ガリレオの落体の法則

理想気体の法則

シュレディンガー方程式と原子の構造

ネーターの定理：エネルギー保存則は対称性から導かれる

受け取る太陽エネルギーは傾斜角によって変化する

なぜ大理石は木よりも冷たいのか？

なぜ質量のない光子がエネルギーを持つのか？

等価原理：重力効果は加速度と区別がつかない

E=mc²：宇宙の4つの基本概念を再考する

太陽の重さを測る方法

自由落下の方程式（1604年）

クーロンの方程式（1785年）

エントロピーに関するボルツマンの方程式（1877年）

ニュートンの三法則が古典力学をどのように説明するか