最終更新：2023年2月15日

クーロン vs ニュートン：宇宙の力の神秘的な類似性

2つの力、1つの数学的構造

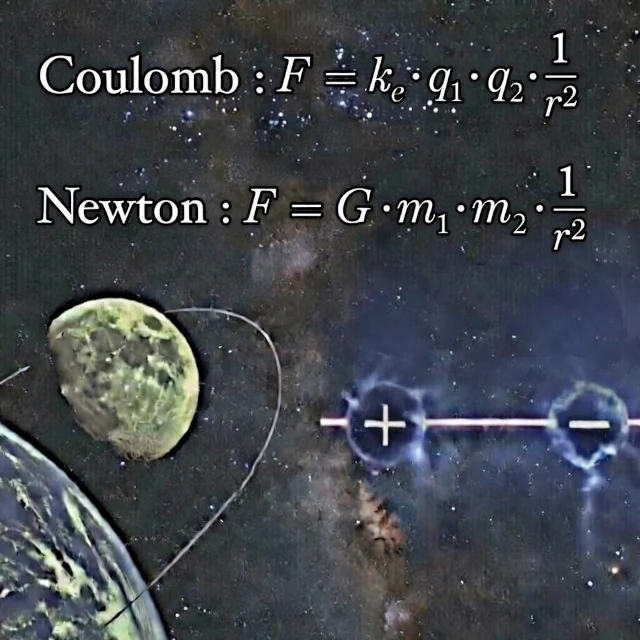
なぜ月は地球の周りを回るのか？なぜ毛織りの帽子を脱いだ後、髪の毛が逆立つのか？この2つの一見無関係な質問の答えは、ほぼ同じ数学的構造で書かれています。一方は、17世紀末にアイザック・ニュートン（1643-1727）によって定式化された万有引力の法則。もう一方は、18世紀末にシャルル・オーギュスタン・ド・クーロン（1736-1806）によって確立された静電気の法則。両方とも「距離の逆二乗の法則」です。

重力の場合：\( F_g = G \cdot \frac{m_1 \cdot m_2}{r^2} \)
電気の場合：\( F_e = k_e \cdot \frac{q_1 \cdot q_2}{r^2} \)

これらの方程式では、\( F \) は力、\( m \) は質量、\( q \) は電荷、\( r \) は2つの物体間の距離を表します。定数 \( G \) と \( k_e \) は単なるスケーリング要因です。この驚くべき類似性は宇宙的な偶然なのか、それとも宇宙の構造に関するより深い真実の兆候なのでしょうか？

三次元空間の幾何学的秘密

この類似性の最も根本的な理由は幾何学的です。

私たちは三次元空間に生きています。質量または電荷である点源の影響を想像してください。この影響は球面的に等方的に（すべての方向で同じように）広がります。

源から距離 \( r \) の場所では、放出された影響のすべてが仮想的な球面を通過しなければなりません。なぜ表面であって体積ではないのでしょうか？影響は球面波の前線のように広がるからです。ある瞬間に、源から同じ距離 \( r \) にあるすべての点は同時に影響を受けます。これらの点はちょうど球面を形成し、体積ではありません。

影響の幾何学的希釈

球の表面積は公式 \( 4\pi r^2 \) で与えられます。エネルギーまたは効果の強度（フラックスと呼ばれる）は、源から離れるにつれてこの表面に均一に分布します。

源が1秒あたりに放出する影響の総量を \( Q \) （流量）と呼ぶと、距離 \( r \) の点で測定される強度 \( I \) は、この総量を広がる表面積で割ったものになります： \( I = \frac{Q}{4\pi r^2} \)

ロウソクのアナロジー

この式は、離れるほど通過しなければならない表面積が大きくなる（\( 4\pi r^2 \) は \( r \) とともに増加する）ため、単位面積あたりの強度が低下することを意味します。これはちょうどロウソクの光のようなものです：1メートルではある面積を照らしますが、2メートルでは同じ光の量が4倍の面積（\( (2)^2 = 4 \)）を照らさなければならないため、単位面積あたりの光の強度は4分の1になります。

表面積、体積ではない：適切な物理量

体積はここでは関与しません。なぜなら、私たちは三次元空間ではなく、表面上の点での効果を測定しているからです。関連する物理量はフラックスの面密度であり、体積密度ではありません。

数学的分解

この式は2つの部分に分解されます：
- \( Q \) は源のみに依存する定数（放出能力）です。
- \( \frac{1}{4\pi r^2} \) は、影響が球面上にどのように希釈されるかを記述する幾何学的要因です。

数学的には、次のように書き直すことができます：\( I = \left( \frac{Q}{4\pi} \right) \times \frac{1}{r^2} \)

項 \( \frac{Q}{4\pi} \) は与えられた源に対する全体的な定数です。距離に対する依存性は完全に \( \frac{1}{r^2} \) の要因に含まれています。このため、強度は距離の二乗に反比例すると言われます。

クーロンの法則とニュートンの法則への応用

クーロンの法則とニュートンの法則では、同じ構造が見られます：
- クーロンの場合：\( F = k_e \cdot q_1 \cdot q_2 \cdot \frac{1}{r^2} \)
- ニュートンの場合：\( F = G \cdot m_1 \cdot m_2 \cdot \frac{1}{r^2} \)

定数 \( k_e \) と \( G \) は、既に \( \frac{1}{4\pi} \) のような幾何学的要因（適切な単位系、例えば合理化SI単位系）と、相互作用の基本的な性質を含んでいます。

空間が他の次元を持っていたら？

私たちが二次元の宇宙に住んでいた場合、影響は長さ \( 2\pi r \) の円（周囲）に分布し、法則は \( I = \frac{Q}{2\pi r} = \left( \frac{Q}{2\pi} \right) \times \frac{1}{r} \) 、すなわち \( 1/r \) の法則になります。四次元では、\( 1/r^3 \) の法則に従います。逆二乗の法則は、三次元空間で伝播する力の数学的な署名です。

しかし、宇宙はそれほど単純ではありません

数学的形式は同じでも、これら2つの力の深い性質は根本的に異なります。最初の違いは明らかです：質量は常に正であるため、重力は常に引力です。一方、電荷は正または負になり得ます。したがって、電気的相互作用は引力でも斥力でもあり得ます。

クーロンの法則の二面性

このように、クーロンの法則には私たちの現実を構成する2つの相補的な側面があります：

引力は反対の電荷間で電子を原子核の周りに保ち、原子を形成します。
斥力は同じ電荷間で原子が融合するのを防ぎ、物質に固体としての一貫性を与えます（あなたの手はテーブルを通り抜けることはできません）。

この二面性がクーロンの法則を物理学の最も優雅で基本的な柱の一つにしています。これがなければ、宇宙は構造も生命もテーブルもない、区別のつかない粒子のスープでしかありません。

2つ目の違いは強度にあります。電気的な力は重力よりもはるかに強力です。これを確認するには、2つの陽子間の電気的反発力と重力引力を比較してください。その比率は電気の方が \( 10^{36} \) 倍も強いです。重力が惑星や銀河のスケールで支配的なのは、物質が大規模には電気的に中性であるためです。正と負の電荷が相殺し合い、弱いが遍在する重力だけが残ります。

2つの基本的な力の比較表

クーロンの法則とニュートンの法則の比較
性質	重力（ニュートン）	静電気（クーロン）
源	質量（常に正）	電荷（正または負）
力の性質	常に引力	引力または斥力
定数	\( G = 6.674 \times 10^{-11} \, \text{N·m}^2/\text{kg}^2 \)	\( k_e = 8.988 \times 10^9 \, \text{N·m}^2/\text{C}^2 \)
相対的強度	\( 10^{-36} \) （最も弱い）	\( 10^{36} \) （はるかに強い）
遮蔽	不可能（負の質量なし）	可能（電気的中性）
優勢な領域	天文学的（惑星、銀河）	原子および分子

力の統合

この類似性は最も偉大な頭脳を魅了してきました。アルバート・アインシュタイン（1879-1955）は、生涯の最後の30年間を重力と電磁気を統一する「統一場理論」の構築に費やしました。彼は失敗しましたが、その探求は現代物理学への道を開きました。今日、私たちはこれら2つの力がより深い理論の低エネルギーでの現れであることを知っています。

重力は一般相対性理論によって時空の曲率として記述されます。静電気を含む電磁気は量子電磁力学によって記述されます。これら2つの柱（一般相対性理論と量子力学）の統一は、理論物理学の聖杯であり、なぜこれら2つの非常に異なる力が基本的なレベルでこの優雅な数学的構造を共有するのかを理解するための探求です。